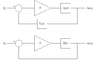
The open loop transfer function is typically represented as G, while the closed loop transfer function is expressed as G/(1 + GH), where H includes any filtering elements. The discussion highlights that open loop systems may appear more stable, but closed loop systems are generally more accurate and less sensitive to component variations. The use of impulse, step, and ramp inputs in control systems is justified as they closely represent real-world scenarios, despite the importance of sine functions in Fourier analysis. The conversation emphasizes the practical applications of these signals in control systems, reinforcing their relevance in analysis and design. Understanding these concepts is crucial for effective control system implementation.