You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
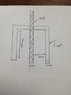
What density do I use to calculate buoyancy for a hollow cylinder float?
- Thread starter mido
- Start date
-
- Tags
- Force
AI Thread Summary
To calculate the buoyancy of a hollow cylinder float, use the density of the fluid it is immersed in, typically water, with a density of 1000 kg/m3. The buoyant force is determined by the volume of the object and the density of the fluid, following the principle that the weight of the displaced fluid equals the buoyant force. While the air density can be considered if the cylinder is in air, for practical purposes, the water density is more relevant. Additionally, the air trapped inside the cylinder may compress under water pressure, slightly affecting the buoyancy calculation, but this is often negligible for general use. Ultimately, the cylinder's ability to float depends on its weight relative to the buoyant force generated by the displaced water.
Physics news on Phys.org
Paradox101
- 47
- 1
What is the fluid it will be immersed in? If it is air, then you should use air density ρ=1.225kg/m3 at 15° to 20°C at sea level.
Buoyancy depends on the density of the fluid and the volume of the object,
FB=ρfluidVobjectg
Buoyancy depends on the density of the fluid and the volume of the object,
FB=ρfluidVobjectg
sophiecentaur
Science Advisor
Homework Helper
- 30,094
- 7,380
As Archimedes is reputed to have said: "the weight of the displaced fluid"
mido
- 9
- 0
it will be immersed in water, it is a hollow cylinder with air trapped in
sophiecentaur
Science Advisor
Homework Helper
- 30,094
- 7,380
The solution to this depends upon how accurate you need the answer. The air/water interface at the bottom is under pressure ρgh and the volume will be less than the cylinder volume, so the upthrust will be less. You may need to account for the volume of air being under water pressure of around 0.3m depth (about 1/30 atmospheric pressure) - which means that the original volume of air will be compressed additionally by about 3% (back of a fag packet calculation). Is that relevant for you? A more accurate answer can be obtained if you are bothered about greater accuracy than a percent.
Otherwise you can say the upthrust will be the volume of the cylinder times the density of water. (minus the actual weight of the material of the cylinder, of course.)
Otherwise you can say the upthrust will be the volume of the cylinder times the density of water. (minus the actual weight of the material of the cylinder, of course.)
Paradox101
- 47
- 1
that is correct, but i don't think he would want to go for THAT accuracy, involving the extra compression of air by 3%. He could simply obtain the volume, plug in the value of ρwater= 1000kg/m3 along with g=9.8m/s2 and voila.sophiecentaur said:The solution to this depends upon how accurate you need the answer. The air/water interface at the bottom is under pressure ρgh and the volume will be less than the cylinder volume, so the upthrust will be less. You may need to account for the volume of air being under water pressure of around 0.3m depth (about 1/30 atmospheric pressure) - which means that the original volume of air will be compressed additionally by about 3% (back of a fag packet calculation). Is that relevant for you? A more accurate answer can be obtained if you are bothered about greater accuracy than a percent.
Otherwise you can say the upthrust will be the volume of the cylinder times the density of water. (minus the actual weight of the material of the cylinder, of course.)
ALTHOUGH yes, i don't think the upthrust would be enough to keep the cylinder afloat
sophiecentaur
Science Advisor
Homework Helper
- 30,094
- 7,380
It would all depend upon how far under the cylinder would go. on that vertical rod. and the mass of the cylinder. My lungs collapse enough to make me neutral at less than 3m depth.
AS with all Engineering matters, the Numbers Count.
AS with all Engineering matters, the Numbers Count.
Similar threads
- Replies
- 9
- Views
- 4K
- Replies
- 7
- Views
- 2K
- Replies
- 4
- Views
- 4K
- Replies
- 1
- Views
- 2K
- Replies
- 5
- Views
- 2K
- Replies
- 26
- Views
- 1K
- Replies
- 10
- Views
- 7K
- Replies
- 6
- Views
- 533
- Replies
- 3
- Views
- 1K
- Replies
- 7
- Views
- 2K
Hot Threads
-
I 'Set of pearls' mathematics / physics help
- Started by lostsoul13
- Replies: 8
- Other Physics Topics
-
B Is space stretching or is new space being created?
- Started by revnice
- Replies: 39
- Other Physics Topics
-
B How do walk-in freezers not give people hypothermia? [they do]
- Started by SpeedOfLightYagami
- Replies: 6
- Other Physics Topics
-
B Easier to pedal with physics
- Started by Dark85
- Replies: 18
- Other Physics Topics
Recent Insights
-
Insights Why Entangled Photon-Polarization Qubits Violate Bell’s Inequality
- Started by Greg Bernhardt
- Replies: 26
- Quantum Interpretations and Foundations
-
Insights Quantum Entanglement is a Kinematic Fact, not a Dynamical Effect
- Started by Greg Bernhardt
- Replies: 11
- Quantum Physics
-
Insights What Exactly is Dirac’s Delta Function? - Insight
- Started by Greg Bernhardt
- Replies: 3
- General Math
-
Insights Relativator (Circular Slide-Rule): Simulated with Desmos - Insight
- Started by Greg Bernhardt
- Replies: 1
- Special and General Relativity
-
Insights Fixing Things Which Can Go Wrong With Complex Numbers
- Started by PAllen
- Replies: 7
- General Math
-
Insights Fermat's Last Theorem
- Started by fresh_42
- Replies: 105
- General Math