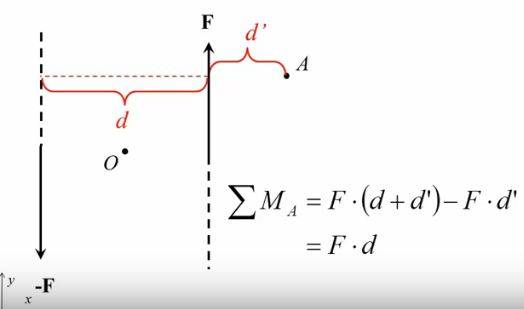
The discussion centers on determining the direction of force acting at point A in a diagram, with a focus on torque calculations. Participants clarify that the equation for net torque at A involves summing moments from two forces, emphasizing that physical contact is not necessary for torque calculations. The conversation highlights the concept of a "couple," where equal and opposite forces create a consistent torque regardless of the reference point. Misleading aspects of the diagram are noted, particularly regarding the representation of forces. Ultimately, the participants reach an understanding of the torque's independence from certain variables, reinforcing the importance of accurate calculations in physics.