What does the square of a differential mean?

[Leo Liu]

Homework Statement

.

Relevant Equations

.

When I was following the calculations of finding the potential energy of a spring standing on a table under gravity, I encountered the integral shown below, where $d\xi$ is the compression of a tiny segment of the spring and $k'$ is the effective spring constant of that segment. The integral sums up the elastic potential energy of each segment along the spring. However, it is not a run of the mill integral in that its differential term is squared. From my experience, the square of a differential is 0, but in this case it obviously possesses some unique properties. Could someone explain why this makes sense? And how do you compute this integral?

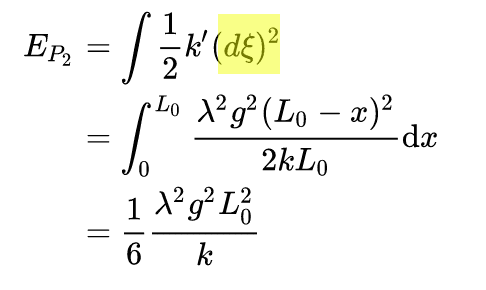
Origin: https://www.zhihu.com/question/324405110/answer/1860254582
In case you need it: https://www.deepl.com/translator

 

[anuttarasammyak]

From your text
k'=A(dx)^{-1} though I am not familiar at all with such a treatment of infinitesimal. Anyway
d\xi=B(dx)
k'(d\xi^2)=C dx
So
\int Dk'(d\xi^2)= \int E dx
as we expect.

 

[mjc123]

I don't think it's helpful to think of it as a square differential. Let's call u(x) the compression of a segment of length δx. Then
u(x) = λg(L₀-x)δx/kL₀
k' = kL₀/δx
Evaluate 1/2 k'u(x)², and THEN (only then) let δx → 0. That's when it becomes a differential.