- #1
DelfinDelfin
- 2
- 1
I have a t-shirt with a next print:
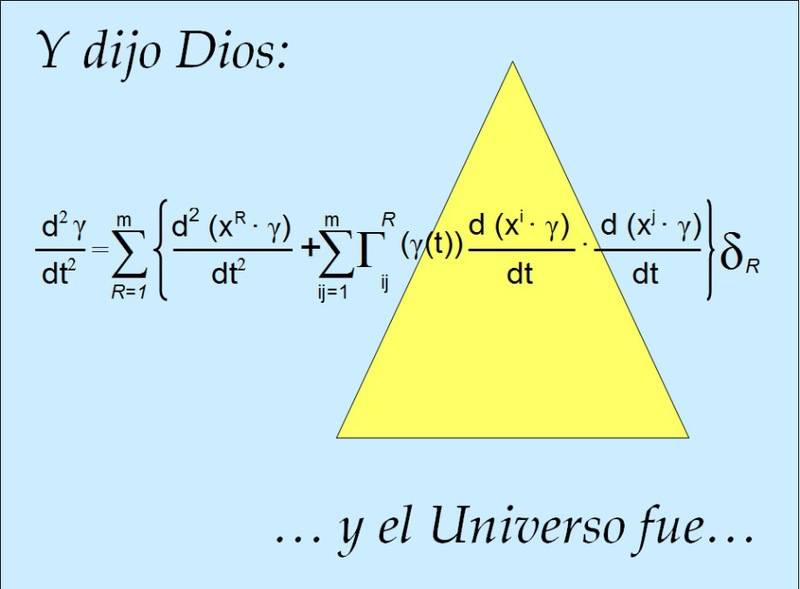
But I am not sure what equation is. I only know that is something related with light. But I haven't found it. I am not sure if it is one from quantum electrodynamics or some advanced course in physics. I would appreciate that somebody could tell me which one is
But I am not sure what equation is. I only know that is something related with light. But I haven't found it. I am not sure if it is one from quantum electrodynamics or some advanced course in physics. I would appreciate that somebody could tell me which one is