What force will be felt by ##B## when a rod is rotated?

[Adesh]

We have a rod $AB$ of mass $m$, a force (perpendicular to AB) is applied at $A$.

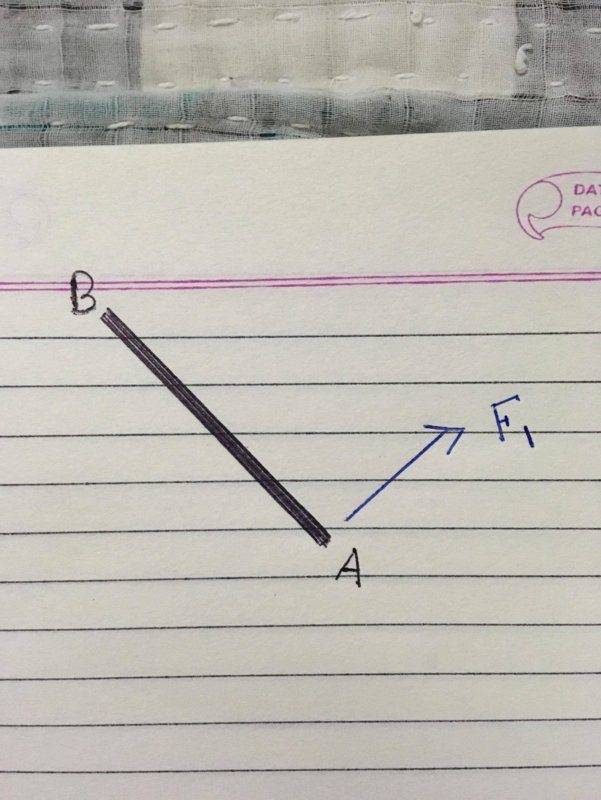
I want to know how much force will $B$ going to feel? When $F_1$ is applied at $A$ rod will rotate about its COM (which lies at the Center) and hence the point $B$ will also move (a little downwards and left). Since, it has moved there must have been some force which would have caused it, what’s that force? (I must mention here that $F_1$ acted only for a very short time, it was momentary, it caused the rotation and went away).

Well, I tried some thoughts. If $B$ were also to act with a force $F_2$ equal in magnitude to $F_1$ like this

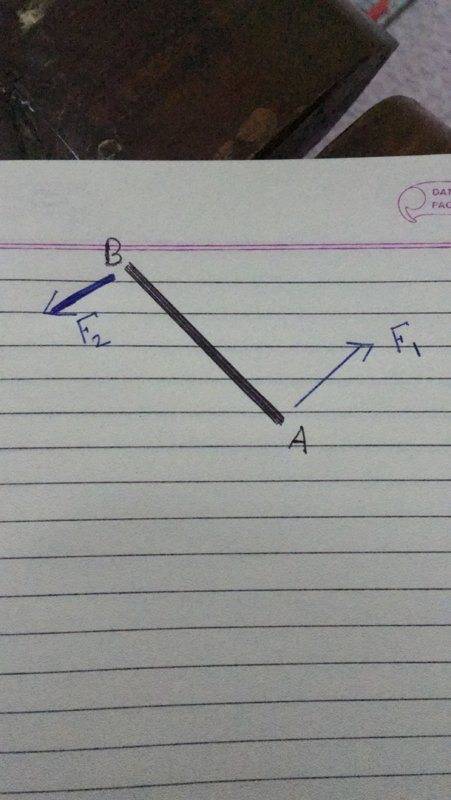
Then also, our system will undergo under same rotation (but under a double torque as before) but this time we know for certain that $B$ was acted by a force $F_2$.

What was the force that caused the $B$ to move in our first case?

 

[A.T.]

What would be the force on $B$ when a force is applied

Force on B by what? Is B just a point, or a finite piece of the rod with non-zero mass?

 

[Adesh]

Force on B by what? Is B just a point, or a finite piece of the rod with non-zero mass?

Well I can fix that by asking “How much force a ball (mass $M$) will experience if it were to kept just next to $B$ (on the side where $B$ would rotate) ?” Everything is frictionless.

 

[A.T.]

Well I can fix that by asking “How much force a ball (mass $M$) will experience if it were to kept just next to $B$ (on the side where $B$ would rotate) ?” Everything is frictionless.

Compute the motion of B, then apply F = ma.

 

[Adesh]

Compute the motion of B, then apply F = ma.

How? Guide me a little more.

 

[Adesh]

Torque/Moment $\tau$ $= \frac{dL}{dt}$, Where $L$ is the angular momentum.
$$ F_1 ~ AB/2 = \frac{dL}{dt} $$
What to do after that?

 

[jbriggs444]

Torque/Moment $\tau$ $= \frac{dL}{dt}$, Where $L$ is the angular momentum.
$$ F_1 ~ AB/2 = \frac{dL}{dt} $$
What to do after that?

You are computing angular momentum $L$ about the midpoint of the rod, yes?

What is the moment of inertia of the rod about its midpoint?

 

[Adesh]

You are computing angular momentum $L$ about the midpoint of the rod, yes?

What is the moment of inertia of the rod about its midpoint?

$\frac{1}{12} m ~AB^2$. So, angular momentum of the rod is $L = \frac{1}{12} m~AB ^2 ~\omega$, where $\omega$ is the angular velocity.

 

[jbriggs444]

$\frac{1}{12} m ~AB^2$. So, angular momentum of the rod is $L = \frac{1}{12} m~AB ^2 ~\omega$, where $\omega$ is the angular velocity.

Since you know the rate of change of angular momentum over time, this puts you in a position to calculate angular acceleration.

 

[Adesh]

Since you know the rate of change of angular momentum over time, this puts you in a position to calculate angular acceleration.

$$ F_1 ~AB/2 = \frac{1}{12}~ AB^2 ~m~ \frac{d\omega}{dt}$$
$$ \frac{6 ~F_1}{AB~m}= \frac{d\omega}{dt}$$

 

[jbriggs444]

$$ F_1 ~AB/2 = \frac{1}{12}~ AB^2 ~m~ \frac{d\omega}{dt}$$
$$ \frac{6 ~F_1}{AB~m}= \frac{d\omega}{dt}$$

Since you now know the angular acceleration, that puts you in a position to calculate the acceleration of the tip of the rod relative to the center of the rod.

You also have Newton's second law to allow you to calculate the acceleration of the center of mass of the rod.

 

[etotheipi]

Well I can fix that by asking “How much force a ball (mass $M$) will experience if it were to kept just next to $B$ (on the side where $B$ would rotate) ?” Everything is frictionless.

I'm a little confused as to the method here. You have a rod which is acted upon by a force $\vec{F}_1$ at end $A$, and a massive ball on the opposite side of the rod next to end $B$. Once the rod is rotated into contact with the ball, the contact force of the ball on the rod will surely also exert a torque on the rod about the centre of mass in the opposite direction to that produced by the force $\vec{F}_1$. Why haven't you included that torque in the angular momentum equation? When you do a Newton II for the centre of mass acceleration, this contact force surely needs to be included also. Isn't this contact force what we're trying to find?

Sorry if I'm missing something!

 

[jbriggs444]

I'm a little confused as to the method here. You have a rod which is acted upon by a force $\vec{F}_1$ at end $A$, and a massive ball on the opposite side of the rod next to end $B$. Once the rod is rotated into contact with the ball, the contact force of the ball on the rod will surely also exert a torque on the rod about the centre of mass in the opposite direction to that produced by the force $\vec{F}_1$. Why haven't you included that torque in the angular momentum equation? When you do a Newton II for the centre of mass acceleration, this contact force surely needs to be included also. Isn't this contact force what we're trying to find?

Sorry if I'm missing something!

There are at least two semi-useful ways to consider the ball on the end of the rod.

You could consider it as a test object, much less massive than the rod. The meaningful number that you get out is nothing more than the acceleration of the rod end multiplied by the mass of the ball.

You could consider it as an anchor point, much more massive than the rod. The meaningful number that you get out is the force required to keep the rod end motionless in the face of the force on the opposite end.

 

[etotheipi]

There are at least two semi-useful ways to consider the ball on the end of the rod.

You could consider it as a test object, much less massive than the rod. The meaningful number that you get out is nothing more than the acceleration of the rod end multiplied by the mass of the ball.

You could consider it as an anchor point, much more massive than the rod. The meaningful number that you get out is the force required to keep the rod end motionless in the face of the force on the opposite end.

Oh, is the ball physically attached to the end of the rod? I thought it was an actual ball positioned slightly to the left of the rod, and that when you rotate the rod you'll whack the ball (or at least, in the time interval of contact, cause it to undergo some acceleration).

Having a rod with a ball as a physically connected point mass type thing on the end makes more sense.

 

[jbriggs444]

Oh, is the ball physically attached to the end of the rod? I thought it was an actual ball positioned slightly to the left of the rod, and that when you rotate the rod you'll whack the ball (or at least, in the time interval of contact, cause it to undergo some acceleration).

Having a rod with a ball as a physically connected point mass type thing on the end makes more sense.

Trying to figure out the force of a whack is a bit of nonsense that we get on these forums from time to time. I wanted to stay as far away from any such interpretation as possible. It would force one into deciding how flexible the rod is, how soft the balls is, how far they started apart, etc. Just not a helpful thing to consider.

I am assuming a light ball just touching the side of the rod end and being pushed by it rather than whacked.

 

[etotheipi]

Trying to figure out the force of a whack is a bit of nonsense that we get on these forums from time to time. I wanted to stay as far away from any such interpretation as possible. It would force one into deciding how flexible the rod is, how soft the balls is, how far they started apart, etc. Just not a helpful thing to consider.

I am assuming a light ball just touching the side of the rod end and being pushed by it rather than whacked.

Though for a light ball ($m \ll M_{rod}$) any force of contact between that ball and the rod is going to produce a large acceleration and the two will then lose contact.

But even without considering the properties of the ball, anchor point or test object, it still seems we need to account for the force of contact between it and the rod. It seems we need a torque of $-R \times \frac{AB}{2}$ in this relation:

$$ F_1 ~AB/2 = \frac{1}{12}~ AB^2 ~m~ \frac{d\omega}{dt}$$

I follow your comments about the interpretation of the results, though am just unsure as to why this force of contact is absent from the model so far.

 

[Adesh]

@etotheipi When I said just “next to the point $B$” it was meant that will be hit by the point $B$ when and only when the point $B$ has rotated and that rotation of $B$ was caused just by the torque $\tau = F_1~ AB/2$.

Now, my question was how much force the ball will experience when $B$ hits it.

 

[Adesh]

@jbriggs444 So, we reached up to here $$\text{Angular acceleration}~ \frac{d\omega }{dt} = \frac{6~F_1}{m~AB}$$

What I should do after this?

 

[jbriggs444]

@jbriggs444 So, we reached up to here $$\text{Angular acceleration}~ \frac{d\omega }{dt} = \frac{6~F_1}{m~AB}$$

What I should do after this?

See post #11.

 

[Adesh]

Since you now know the angular acceleration, that puts you in a position to calculate the acceleration of the tip of the rod relative to the center of the rod.

Since, acceleration of a point is equal to its angular acceleration times the distance of the point from the axis of rotation, i.e. $$ a = \alpha ~ r$$ so, in our case the acceleration of the tip of the rod is $$ a = \alpha ~ AB/2 \\
a = \frac{3~F_1}{m} $$.

You also have Newton's second law to allow you to calculate the acceleration of the center of mass of the rod.

Acceleration $a_{COM} = \frac{F_1}{m}$.

 

[jbriggs444]

Since, acceleration of a point is equal to its angular acceleration times the distance of the point from the axis of rotation, i.e. $$ a = \alpha ~ r$$ so, in our case the acceleration of the tip of the rod is $$ a = \alpha ~ AB/2 \\
a = \frac{3~F_1}{m} $$.

Acceleration $a_{COM} = \frac{F_1}{m}$.

Which puts you in a position to easily compute the acceleration of the rod tip, right?

 

[Adesh]

Which puts you in a position to easily compute the acceleration of the rod tip, right?

Isn’t the acceleration of rod’s tip $\frac{3F_1}{m}$ ?

 

[jbriggs444]

Isn’t the acceleration of rod’s tip $\frac{3F_1}{m}$ ?

No.

That number comes from the rotational acceleration rate. It gives the acceleration of the rod's tip relative to the center of mass.

 

[Adesh]

No.

That number comes from the rotational acceleration rate. It gives the acceleration of the rod's tip relative to the center of mass.

So, is it $$ \frac{3~F_1}{m} - \frac{F_1}{m}= \frac{2F_1}{m}$$

 

[jbriggs444]

Yes.

Obviously the direction will be opposite to the force being applied at the other end.

 

[Adesh]

Yes.

Obviously the direction will be opposite to the force being applied at the other end.

Yes. So, we got the acceleration of the tip of the rod, how we would find the force the ball would experience ?

 

[jbriggs444]

Yes. So, we got the acceleration of the tip of the rod, how we would find the force the ball would experience ?

For a small test ball being pushed continuously by the tip of the rod, Newton's second law applies.

If the ball is big enough to affect the motion of the rod, you have a different problem to solve. You should start by computing the position of the center of mass of the ball+rod.

 

[Adesh]

For a small test ball being pushed continuously by the tip of the rod, Newton's second law applies.

If the ball is big enough to affect the motion of the rod, you have a different problem to solve. You should start by computing the position of the center of mass of the ball+rod.

Will the acceleration from the tip of the rod going to be imparted to the ball? If that is so, we would get $$F = M_{ball} ~\frac{2F_1}{m}$$

 

[jbriggs444]

Will the acceleration from the tip of the rod going to be imparted to the ball? If that is so, we would get $$F = M_{ball} ~\frac{2F_1}{m}$$

Right. As I've said at least twice now, my vision is that the ball is nestled against the tip of the rod, being pushed by it. So it accelerates at the same rate.

 

[Adesh]

Thank

Right. As I've said at least twice now, my vision is that the ball is nestled against the tip of the rod, being pushed by it. So it accelerates at the same rate.

Thank you so much sir, thank you so much. You have helped me very nicely.