What happens when F > 90N in Atwood problem?

[physicsfox]

Here’s a question for you all… but first some background

(see jpeg attachment for sketch)

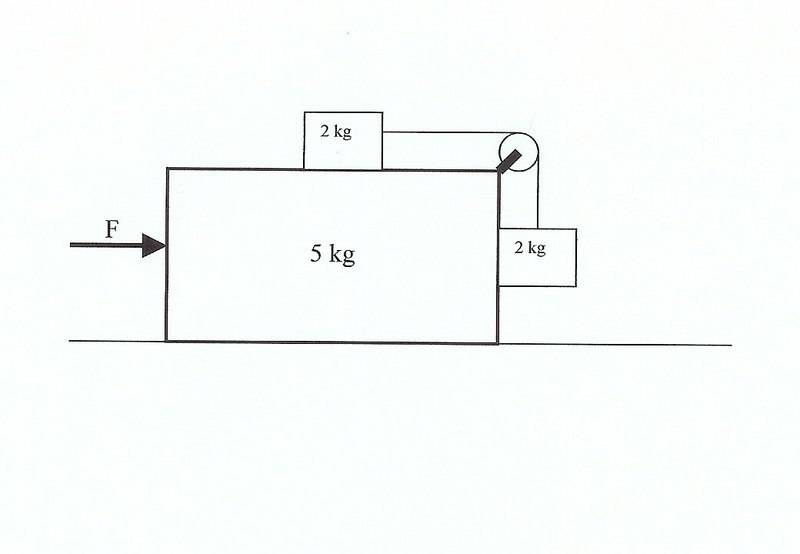
Assuming all surfaces are frictionless (5kg on horizontal surface, two 2kg blocks on 5kg block), and the pulley has no mass, with what horizontal force applied to the 5kg block will the two 2kg blocks remain in the same location relative to 5kg block? In other words, with what applied force, F, will the two 2kg blocks remains “fixed” against the 5kg block (relative acceleration 0)?

If the vertically hanging 2kg block is to remain at the same vertical position as the system accelerates to the right, then the tension above the hanging 2kg block will be equal to the Fg of the hanging 2 kg block. The Tension is 20N. The horizontal 2kg block is therefore being pulled to the right by the same T=20N. The acceleration of the 2kg block is then 10 m/s2 (F=ma). To create that 20N in the horizontal string, the system needs to accelerate at 10m/s2. Thus, F=90N. (F=ma=9kg*10m/s2).

Now the question. Assuming the above is correct, what would happen if the applied horizontal force was, let’s say, 100N? Qualitatively, the two 2kg blocks would not remain at the same position relative to the 5kg block. The horizontal 2kg block would move towards the back of the 5kg block, and the vertical 2 kg block would rise up. Would the two blocks have a relative acceleration? I would think so. But how would you quantify this acceleration? How would you quantify the acceleration of the 5kg block? Is the 100N pushing the entire mass (9kg), or does the relative acceleration of the two 2kg blocks have some affect that I am not considering?

I would appreciate any thoughts on this.

 

[BerryBoy]

OK, so its asking for the Force that needs to be applied horizontally to the system so that the acceleration of the 2 masses (with respect to the block) is 0.

Think about tension in the horizontal and vertical parts of the chords.
Think about WHAT this horizontal force applied would accelerate.
Think about the acceleration of the top mass if the block were NOT moving. (this is the main point to think about).

Try to show some working please, we can't help much if we don't know how much you know.

Regards,
Sam

 

[physicsfox]

In response to "BerryBoy's" post, I have answered the original question, and have shown the detail in my original posting. As an extension to the original question, assuming that a 90N horizontal force is the force that will result in the atwood and the block having a relative acceleration of zero, what would the acceleration of the atwood be, relative to the 5kg block, if 100N is applied to the 5kg block? If the 2kg block on the front vertical edge of the block rises up... or accelerates up... wouldn't the tension be greater than 20N? And if so, how would you calculate this?

So, again, this is just an extension of a question I have already answered. I am just exploring the topic a little more. I would appreciate any thoughts about this question. Thanks.

 

[Fermat]

Hi Physicsfox, nice problem.

I checked over your analysis and agree with it and your end result. The 90 N.

In the general case, the two small blocks move wrt the big block. When F > 90N, (with the mass values you specified) then the small blocks move "backwards" with an acceleration relative to the big block. And when F < 90, then they accelerate forwards relative to the big block.

When I solved this problem, I split up the accelerating force F, into two components, giving F = F' + T, where F' is the component of F that accelerates M and m2 (the hanging block) and T is the component of F that accelerates the m1 block (on top of M). T is also the tension in the string over the pulley.