What Happens When You Identify Points on a Torus and a Rolled Cylinder?

[ehrenfest]

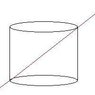
What is the space resulting from the identification (x,y) ~ (x+2piR, y+2piR)? How is it different from the space resulting from
(x,y) ~ (x+2piR, y)
(x,y) ~ (x, y+2piR), which is a two-dimensional torus (a donut)

 

[f-h]

It's a cylinder, rolled up along the diagonal.

 

[ehrenfest]

What diagonal?

 

[CompuChip]

I'd say the diagonal indicated on the attachment (up to symmetry )

 

[ehrenfest]

Sorry, I don't see any attachment. Was that just a joke?

 

[CompuChip]

No, I forgot to click upload. Apparently you posted while I added it.

(BTW: Post 13^2 for me)

 

[ehrenfest]

13^2

Why would you ask me to post that?

 

[jim mcnamara]

He meant he hit post #169, he did not want you to post anything.

 

[f-h]

Take (x,y) to (x+a,y+a) and you move up parallel to the diagonal between the x and the y axis. if you identify after a = 2Pi then you get a cylinder rolled along that diagonal.

 

[George Jones]

ehrenfest, what happens if you switch to coordinates x' = (x + y)/sqrt(2) and y' = (x - y)/sqrt(2)?

 

[ehrenfest]

I see why it is different than the other identification! The R has to be the same for both x and y.

If you switch to light-cone coordinates, then it is a cylinder rolled around the y' axis, right?