annao
- 3
- 0
Homework Statement
A plank of wood sits on top of two rollers with radius of 44.4 cm. The plank is pulled forward so it moves at a constant acceleration of 2.24 m/s^2, starting from rest, and the rollers roll without slipping along the ground and in contact with the plank. What is the angular speed of the rollers after 1.14 s? Express your answer in rad/s.
Homework Equations
w=wo+
The Attempt at a Solution
wo=0 rad/s; t=1.14 s; a=2.24 m/s^2; r=0.444 m
w=wo+
w=5.75 rad/s
Am I on the right track? Do I need to divide by 2 because there are two rollers?
Thank you
Attachments
-
 Rollers.png4.4 KB · Views: 350
Rollers.png4.4 KB · Views: 350 -
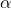 media%2Ffe6%2Ffe688a78-1523-4a26-89e0-03c6816c6024%2F49a6e28c-9948-4ec2-84cb-e0ffc07e1ff9.png187 bytes · Views: 298
media%2Ffe6%2Ffe688a78-1523-4a26-89e0-03c6816c6024%2F49a6e28c-9948-4ec2-84cb-e0ffc07e1ff9.png187 bytes · Views: 298 -
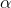 media%2Ffe6%2Ffe688a78-1523-4a26-89e0-03c6816c6024%2F49a6e28c-9948-4ec2-84cb-e0ffc07e1ff9.png187 bytes · Views: 310
media%2Ffe6%2Ffe688a78-1523-4a26-89e0-03c6816c6024%2F49a6e28c-9948-4ec2-84cb-e0ffc07e1ff9.png187 bytes · Views: 310 -
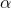 media%2Ffe6%2Ffe688a78-1523-4a26-89e0-03c6816c6024%2F49a6e28c-9948-4ec2-84cb-e0ffc07e1ff9.png187 bytes · Views: 290
media%2Ffe6%2Ffe688a78-1523-4a26-89e0-03c6816c6024%2F49a6e28c-9948-4ec2-84cb-e0ffc07e1ff9.png187 bytes · Views: 290 -
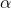 media%2Ffe6%2Ffe688a78-1523-4a26-89e0-03c6816c6024%2F49a6e28c-9948-4ec2-84cb-e0ffc07e1ff9.png187 bytes · Views: 338
media%2Ffe6%2Ffe688a78-1523-4a26-89e0-03c6816c6024%2F49a6e28c-9948-4ec2-84cb-e0ffc07e1ff9.png187 bytes · Views: 338