disk256
- 2
- 0
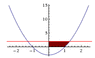
The area of the region bounded by the curve y = 3x^2-3 , the y-axis, x-axis, and the line
x = 2 is equal to
so far i ve managed to draw the graph i m getting a value of 9
is that correct
x = 2 is equal to
so far i ve managed to draw the graph i m getting a value of 9
is that correct