So, I think this is the situation you are talking about (on decreasing the angle between the line joining the centres and path of the ball (red), number of bounces increases),
View attachment 282741
This infact, does contradict what I thought earlier the situation would be for a ball striking the far post below the midpoint,
View attachment 282747
But on closer inspection, I spotted a difference between the two,
View attachment 282743View attachment 282744
We can quite clearly see that on extending the path of the ball, the red one passes above the centre, while the blue one passes below the centre.
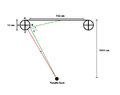
So, I speculate this (below) might be the correct limiting case (feel free to correct me),
View attachment 282745
Here the path passes through the centre of the far post and on rebounding off the far post, the path of the ball retraces itself.
Am I getting it right this time?