Physicscookie
- 3
- 1
Member warned to use the formatting template for homework posts.
I present the following problem to my AP and have received a variety of answers, being a new physics teacher I am not sure that my answer is correct. I would love to see the solution and justification.
Thanks
One attempt based on the inference that one block is gaining U (A) and the other (B) 1 is loosing it
1/2 mv2 b - 1/2 mv2a = 4.5 J
In the figure below, the pulley is massless, and both it and the inclined plane are frictionless. The masses are released from rest with the connecting cord taut. Some time later the 2.0 kg block has a speed of 3 m/s. What was the change in potential energy of both blocks?
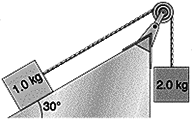
Thanks
One attempt based on the inference that one block is gaining U (A) and the other (B) 1 is loosing it
1/2 mv2 b - 1/2 mv2a = 4.5 J
In the figure below, the pulley is massless, and both it and the inclined plane are frictionless. The masses are released from rest with the connecting cord taut. Some time later the 2.0 kg block has a speed of 3 m/s. What was the change in potential energy of both blocks?