What is the Coefficient of Friction in Conservation of Energy Problem?

[Karol]

Homework Statement

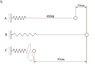
A spring with a constant k=10[N/m] is attached with a long rope to a weight of 0.05 kg. they both lie horizontally on the table. the string is stretched 10 cm and released and the weight travels 40 cm on the table until it halts. what is the coefficient of friction

Homework Equations

Elastic energy of spring:E_P=\frac{1}{2}kx^2

The Attempt at a Solution

Conservation of energy:
\frac{1}{2}kx^2=mg\mu\cdot \triangle x
\frac{1}{2}10\cdot 0.1^2=0.05 \cdot 10 \cdot \mu \cdot 0.4 \rightarrow \mu=0.25
The answer should be μ=0.2

 

[NascentOxygen]

With friction present, the spring may end up still stretched a bit.

 

[Karol]

I don't see how this can happen in this case since the spring gives velocity to the mass which continues travelling.
In any case the initial potential energy of the spring is the same, it is stretched 10 cm.

 

[NascentOxygen]

If the spring remains stretched a bit, it retains some potential energy.

 

[Karol]

The spring will stop at a distance of:
F=mg\mu=kx\rightarrow 0.5\mu=10x \rightarrow x=0.05\mu
Conservation of energy:
\frac{1}{2}k \left(0.1^2-0.05^2\mu^2\right)=mg\mu\triangle x
5(0.01-0.0025\mu^2)=0.5\mu 0.4
0.0125\mu^2+0.2\mu-0.05=0 \rightarrow \mu=0.246
It still isn't μ=0.2

 

[rude man]

Right now I don't see how the problem can be solved unless the coefficient of static friction is also given.

We start to pull on the spring. At first, the block stays put. At some spring stretch level the block starts to move. This will happen long before the full 10 cm of spring tension is reached since at 10cm the spring force is 1N, way more than what is required to start the weight moving even for a high static friction coefficient. So we have to continue pulling on the spring even when the weight has started to accelerate, until the full 10cm of spring tension is reached. So the puller applies not only the energy in a 10cm-expanded spring but also his force x distance until the 10 cm spring extension is reached.

That is the total system input power. The system output power is of course weight x kinetic friction coefficient x distance traveled after the spring is released.

A pretty complicated problem and I wonder if the wording is correct.

 

[Karol]

We start to pull on the spring. At first, the block stays put. At some spring stretch level the block starts to move.

The system isn't like that. you don't start to pull the spring until the mass also moves, no. you pull the mass which pulls the string through the rope. i knew my simple drawing isn't good enough.
You pull the mass, which stretches the spring, a distance of 10cm and release.

 

[Karol]

Installation

There can be no residual elongation of the spring because of the installation. the spring is pulled by a long cord. at the end of the cord is the mass. the mass is released and it travels until it stops, in front of the spring.

 

[NascentOxygen]

There can be no residual elongation of the spring because of the installation. the spring is pulled by a long cord. at the end of the cord is the mass. the mass is released and it travels until it stops, in front of the spring.

Right. I hadn't looked at this closely enough. It' doesn't seem complicated. The spring gives up all its energy. The mass travels 40cm.

So your calculations seem right. μ_k = 0.255

Maybe one of the data values isn't right? e.g., say the mass travels 51cm ...

 

[rude man]

OK, with this picture I don't see why your original answer isn't correct. Hope you can post what you found out later about it.

EDIT: I'll bet the spring traveled 40 cm from its original position. That makes Δx = 0.4 + 0.1 = 0.5 and then the answer is indeed μ = 0.2.