- #1
SSG-E
- 60
- 12
- TL;DR Summary
- In case of right angled triangles, C^2 = A^2 +B^2 - 2AB cos(Ψ) is shortened to C^2 = A^2 +B^2 because the cosine of the angle "Ψ" which is 90° is equal to 0. But how is its cosine equal to 0.
I
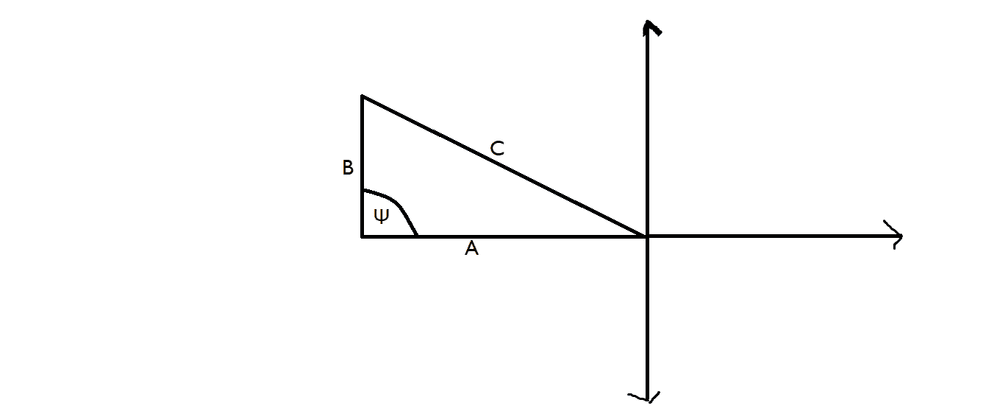
Not Correct.But how is its cosine equal to 0.
You can find the proof of Law Of Cosines in some Trigonometry books and some Calculus books. There is an old book by Anton which includes a proof.SSG-E said:Summary:: In case of right angled triangles, C^2 = A^2 +B^2 - 2AB cos(Ψ) is shortened to C^2 = A^2 +B^2 because the cosine of the angle "Ψ" which is 90° is equal to 0. But how is its cosine equal to 0.
IView attachment 264987
SSG-E said:Summary:: In case of right angled triangles, C^2 = A^2 +B^2 - 2AB cos(Ψ) is shortened to C^2 = A^2 +B^2 because the cosine of the angle "Ψ" which is 90° is equal to 0. But how is its cosine equal to 0.
neilparker62 said:cos 90 = sin(90-90) = sin(0) = 0.
Does that now beg the question "how is sin(0) = 0" ?
mathwonk said:My favorite proofs are propositions 12, 13 Book II, Euclid's Elements.
etotheipi said:Another way, label the triangle like this:
View attachment 265361
Pythagoras on the left triangle: ##x^2 + h^2 = b^2##
Pythagoras on the right triangle: ##a^2 - 2ax + (x^2 + h^2) = c^2##
Now since ##b\cos{C} = x##, we finally have ##a^2 + b^2 - 2ab\cos{C} = c^2##.
Adesh said:Oh you English people! I can see that you have not even used the scale for drawing that perpendicular ##h## and that ##h## is very pointy, it has sharp end points. It’s really an English’s writing (so tough to read).
Leo Liu said:Draw an unit circle and add an additional line on the positive y-axis as the terminal arm. Let z denote the length of the terminal arm, we get: $$\cos(x)=\frac x z\implies \cos(90)=\frac 0 1 = 0$$
I'm pretty sure that he means the ray whose angle is measured relative to the reference direction, the positive x-axis.etotheipi said:What do you mean by a terminal arm?
##h=b\sin\hat{C}## and ##x=b\cos\hat{C}##. Hence:etotheipi said:Another way, label the triangle like this:
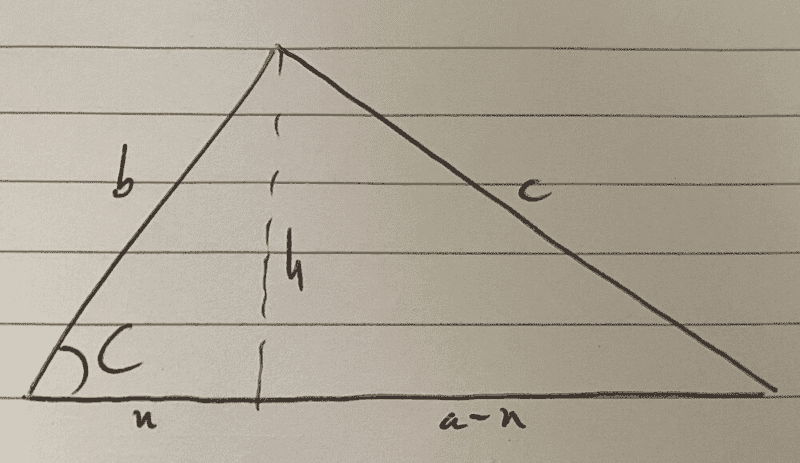
Pythagoras on the left triangle: ##x^2 + h^2 = b^2##
Pythagoras on the right triangle: ##a^2 - 2ax + (x^2 + h^2) = c^2##
Now since ##b\cos{C} = x##, we finally have ##a^2 + b^2 - 2ab\cos{C} = c^2##.
It is a great loss of archaeology that you do not work in that field.neilparker62 said:##h=b\sin\hat{C}## and ##x=b\cos\hat{C}##. Hence:
$$c^2=b^2\sin^2\hat{C}+(a-b\cos\hat{C})^2=a^2 + b^2 - 2ab\cos{\hat{C}}$$, and as a 'bonus': $$\tan\hat{B}=\frac{b\sin\hat{C}}{a-b\cos\hat{C}}$$It
thanks - cool profile pic by the way. Where is it from ?Leo Liu said:It is a great loss of archaeology that you do not work in that field.
I found it on a website for sharing wallpapers.neilparker62 said:
The Law of Cosines is a trigonometric formula that relates the lengths of the sides of a triangle to the cosine of one of its angles. It can be used to solve for missing side lengths or angles in a triangle.
The Law of Cosines is used when solving triangles that do not have a right angle. It is particularly useful when you know the length of two sides and the measure of the included angle, but need to find the length of the third side or another angle.
The formula for the Law of Cosines is c² = a² + b² - 2ab cos(C), where c is the length of the side opposite the angle C, and a and b are the lengths of the other two sides.
The Law of Cosines can be derived from the Pythagorean Theorem and the Law of Sines. By substituting the formula for the sine of an angle into the Pythagorean Theorem, you can manipulate the equation to get the Law of Cosines.
The Law of Cosines has many practical applications, such as in navigation and surveying. It can be used to find the distance between two points on a map, or to determine the height of a building or mountain. It is also used in physics and engineering to calculate forces and vectors.