What is the correct answer for the electric charge question?

In summary: Because English is my second language, so that it is hard for me to recognize what it is, if i don't have pictures :DIn summary, electric charge question states that there is an electric field inside an insulator, but the answer is not correct because the field still exists. A is the correct answer.
  • #1
cuongbui1702
31
0
Electric charge question[Updating...]

1)
testbank-28-chap21_zps8fb3ad78.png

I tried to do this homework, but my answer is all , of course it is not as same as this question's answer. That is my procedure:
+) First, 2 charged have a same chagre Q, after these also have a same charge q=(Q-Q').
+) F'/F=[(Q-Q')/Q]^2.
+) I substituting all answer, and it is correct all, i can have 1 Q'.
Why the answer is C.

2)
testbank-28-chap21_zps9b70a217.png

F=Q.q/4piE(a^2+d^2)
F max when a^2+d^2 min=> d^2 min when d=0 why the answer is E, i think a true answer is A

3)
testbank-44-chap21_zps5e707e6d.png

Following my textbook:
testbank-44-chap21_zps07104445.png

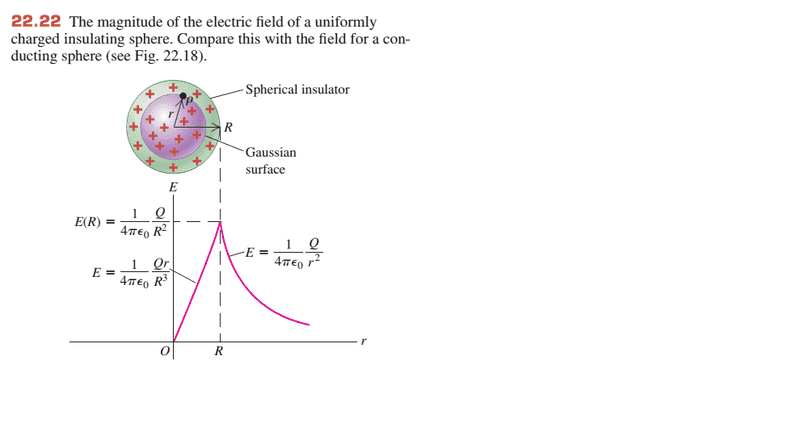
it is also existing an electric field inside a insulator. So the answer E is not correct, because it still have Electric force. I think A is true. Am I right?
 
Last edited:
Physics news on Phys.org
  • #2
cuongbui1702 said:
1)
I tried to do this homework, but my answer is all , of course it is not as same as this question's answer. That is my procedure:
+) First, 2 charged have a same chagre Q, after these also have a same charge q=(Q-Q').
+) F'/F=[(Q-Q')/Q]^2.
+) I substituting all answer, and it is correct all, i can have 1 Q'.
Why the answer is C.
Let Q be the initial charge on A and B. (Express the initial force F in terms of Q.) When C touches A, what are the resulting charges on A and C? Then when C touches B, what are the resulting charges on C and B? Once you have the final charges on A and B expressed in terms of Q, then find an expression for the new force between A and B.
 
  • #3
To get a resulting charges on A and C or B and C i think it is quite hard, or i don't know to calculate it
 
  • #4
cuongbui1702 said:
To get a resulting charges on A and C or B and C i think it is quite hard, or i don't know to calculate it
No, it's easy. And unless you know how it works, you cannot solve the problem.

Here's how it works: When two identical conducting spheres are touched, the total charge distributes uniformly between the two of them.
 
  • #5
Oh thank you, that is amazing thing i have learned today, i got the answer, it is as same as with this( sorry about my terrible English). Why i can't see this in my textbook University Physics with Modern Physics, 13th Edition of Young and Freeman
 
  • #6
Who can help me Question2 and 3, please
 
  • #7
cuongbui1702 said:
2)
F=Q.q/4piE(a^2+d^2)
F max when a^2+d^2 min=> d^2 min when d=0 why the answer is E, i think a true answer is A
You need an expression for x-component of the force, not the total force.

(Don't keep adding problems to the original post. That makes things confusing to follow and respond to. Best to solve one problem before starting another; usually best to have one problem per thread, unless they are very related.)
 
  • #8
cuongbui1702 said:
3)
Following my textbook:

it is also existing an electric field inside a insulator. So the answer E is not correct, because it still have Electric force. I think A is true. Am I right?
No, you are not right. The illustration from the book describes a uniformly charged sphere, but the problem is about a spherical shell (a balloon).
 
  • #9
Doc Al said:
You need an expression for x-component of the force, not the total force.

(Don't keep adding problems to the original post. That makes things confusing to follow and respond to. Best to solve one problem before starting another; usually best to have one problem per thread, unless they are very related.)
- Oh, I read wrong problem :(. But, when i did it again, my process is long(i use derivatives), maybe in this question, i substituting all answers is faster than my process.
- I am scared, admin delete my post when i make a lot of question :(
 
  • #10
Doc Al said:
No, you are not right. The illustration from the book describes a uniformly charged sphere, but the problem is about a spherical shell (a balloon).

What is the difference between them??
 
  • #11
cuongbui1702 said:
What is the difference between them??
A balloon is hollow shell with nothing inside. The text from your book describes a solid sphere of charge, not just a shell.
 
  • #12
cuongbui1702 said:
- Oh, I read wrong problem :(. But, when i did it again, my process is long(i use derivatives), maybe in this question, i substituting all answers is faster than my process.
I suggest you actually work it out with derivatives; it's not that bad and it simplifies quickly.
 
  • #13
Doc Al said:
A balloon is hollow shell with nothing inside. The text from your book describes a solid sphere of charge, not just a shell.
Because English is my second language, so that it is hard for me to recognize what it is, if i don't have pictures :D
 
  • #14
Doc Al said:
No, it's easy. And unless you know how it works, you cannot solve the problem.

Here's how it works: When two identical conducting spheres are touched, the total charge distributes uniformly between the two of them.

Doc AI, i have a same problem but my answer is not as same as question's answer. Following you, it must be A.
testbank-27-chap23_zps1c18ff99.png
 
  • #15
cuongbui1702 said:
Doc AI, i have a same problem but my answer is not as same as question's answer. Following you, it must be A.
In this example, the conducting spheres are not identical. (The more general principle is that the potential will be the same after they touch.)
 

FAQ: What is the correct answer for the electric charge question?

What is electric charge?

Electric charge is a fundamental physical property of matter that causes it to experience a force when placed in an electromagnetic field. It is measured in units of coulombs (C) and can be either positive or negative.

How is electric charge created?

Electric charge is created when atoms gain or lose electrons, resulting in an imbalance of positive and negative charges. This can occur through friction, contact, or induction.

What is the difference between static and current electricity?

Static electricity is the buildup of electric charge on the surface of an object, while current electricity is the continuous flow of electric charge through a conductor. In static electricity, the charge remains in one place, while in current electricity, it moves from one point to another.

What are the different types of electric charge?

There are two types of electric charge: positive and negative. Protons have a positive charge and electrons have a negative charge. Objects with the same type of charge repel each other, while objects with opposite charges attract each other.

How is electric charge related to electric fields?

Electric charge is the source of electric fields, which are the force fields that surround charged objects. The strength of an electric field is determined by the amount and distribution of electric charge in the surrounding area.

Similar threads

Electric field external to Conducting Hollow Sphere with charge inside
Replies
23
Views
2K
Electric field created by point charges
Replies
6
Views
310
Electric field strength at a point due to 3 charges
Replies
3
Views
1K
Finding the position where the electric field is zero
Replies
2
Views
939
Electric field of point along the central vertical axis of a triangle
Replies
3
Views
442
Charge on a grounded conducting sphere in a uniform electric field, after ungrounding and movement
Replies
1
Views
772
Minimizing the Energy of Two Conductors Very Far Apart
Replies
23
Views
964
E&M: Forces resulting from Charges at the Corners of a Cube
Replies
13
Views
1K
Electric field at a point inside a non-uniformly charged sphere
Replies
6
Views
710
Method of mirroring - metal plates
Replies
11
Views
1K

Hot Threads

Recent Insights

Back
Top