What is the direct of the induced current in the circular loop

[wazzup]

I'd really appreciate some help with the following questions.

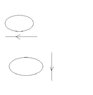
Q1) What is the direct of the induced current in the circular loop due to the current shown in each part of the following fig?Have attached pics of 2 questions. The one on top has I increasing and one on the bottom has I decreasing.

HOw do I go about getting it?

For the first one, I get the external magnetic field to be going downward ( intot he paper ) but then how do I find the induced magnetic field since the decreasing current does not tell me anything about the flux?
______________________________________________________________________________________________________

q2) A 10.2 cm diameter wire coil is initially oriented so that its plane is perpendicular to a magnet field of .63T pointing up. During the course of .15s, the field is changed to one of .25T pointing down. What is the average induced EMF in the coil?

I did the followng:-( [(.63)(3.14)(.102/2)^2] - [(.25)(3.14)(.102/2)^2]) / (.15) and got .021V. Is this correct?

Thanks

 

[mezarashi]

The decreasing and increasing currents do tell you information about the magnetic field in the wire's vicinity: by Ampere's Law. The right hand rule can then be used to determine the direction of the magnetic field.

To determine which direction the current in loop flows, use another right hand rule. Your thumb pointing in the direction of "change of flux". The current will follow the curve of your hand. This "change of flux can be thought of as the direction of the flux if you leave the situation to be for an infinite duration.

For example in the top loop, the increasing current will cause a larger flux in the direction going into the paper, and your thumb points into the paper. That is, if you left the current to keep increasing, there is no doubt that the flux would continue to be into the paper.

For the bottom example, the decreasing current weakens the flux going into the paper, and your thumb points up. If you continue to let the current decrease and eventually reverse, the flux would no longer be into the paper, but out of it, thus the change is in the out of the paper direction.

 

[lightgrav]

The induced Electric field encircles the NEGATIVE change of B-field
(same geometry as Magnetic field encircling a current that pierces Area).
Thumb should point OUT of the paper (at loop) in diagram 1,
since B points into paper (thru loop) , so CHANGE in B-field is into paper ,
so finally the NEGATIVE change in B points OUT through the loop Area.
Right-hand fingers wrap counter-clockwise to encircle this - d(B.A)/dt .