What is the effect of a wire with current on Ampère's circuital law?

[valjok]

Revising my old university lectures, I have encountered the famous law of magnetic field around a closed loop:
\oint_L \mathbf{H} \cdot \mathrm{d}\boldsymbol{\ell} = \sum I

The integral is simplified down to a product Hl when the perfectly round loop is orthogonal to the current. In this case H is constant on the loop and length of a circle l = 2 Pi r, wherefrom we can derive the \mathbf{H} = \frac{I}{2 \pi r}.
For instance, if the first current goes into the screen while another comes out of it, we can compute the field at point R, which distance is r from both currents:

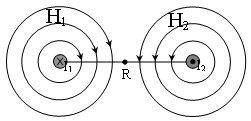
H_R = H_{1R} + H_{2R} = (I_1 + I_2)/2\pi rAs I understand the writing, it allows us to compute the field in any point by just summing H from all circles orthogonal to the current direction. Everything looks fine until a wire of current is considered:

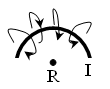
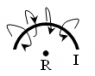
Here, a wire with current I surrounds the point R. The wire consits of infinitely many points and there is the current in every point, so that each point of wire contributes a finite amount of field to R, resuling in infinite H. I suspect that my treatment of shape of current is too loose in the fromula Hl = I and must be clarified.

 

[Meir Achuz]

The simple formula HL=I cannot be used for a current loop, because the loop does not have the appropriate symmetry. The law of Biot-Savart for a current loop gives
H=I/2r.

 

[valjok]

Thank you, I have realized that my simplified formula describes the infinitely long stright line of current. This makes the fied round symmetric around it. Bending the wire distorts the field breaking its circle shape, the H becomes stronger in the center and the formula cannot be applied anymore. The infinite sum occurs when infinite number of stright current lines will be put tangently to the curve around the R :)