What is the formula for calculating tributary areas in a slab on beam?

[dahoa]

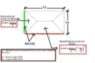
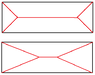
I'm trying to derive these formulas of tributary areas of a slab on beam. The idea is simple.. portions of the rectangle is distributed to the edge by the formulas.. but inside a pure triangle area.. how do you compute for the 2 triangular areas and 2 trapezoidal areas?

 

[mfb]

I don't understand the context, but the area is easy to find if you know how far away from the left (right) side the left (right) inner vertex is. The area of the triangles is just 1/2 * Lx * (this unknown distance). The area of the trapezoidal parts is then the total area minus the area of the triangles, divided by 2 (because you have two of them).

 

[dahoa]

the formula is for moment..

I found out an alternative formula to get the area of the trapezoidal is just Lx/4 * (2- Lx/Ly)... I understood where the Lx/4 comes from... but how is the (2 - Lx/Ly) derived? I need to know this specifically and not just other ways to get the trapezoidal which you say is just deducting the triangles and dividing by two.

 

[mfb]

First you have to tell us how to determine where the points are. See the attached sketch. It is clear that the triangles have different areas, but both have the same overall shape as your sketch. Do you know some additional length, angle or something similar?

I found out an alternative formula to get the area of the trapezoidal is just Lx/4 * (2- Lx/Ly)

That can lead to negative values and it doesn't even have the units of an area.

 

[dahoa]

First you have to tell us how to determine where the points are. See the attached sketch. It is clear that the triangles have different areas, but both have the same overall shape as your sketch. Do you know some additional length, angle or something similar?

View attachment 227743

That can lead to negative values and it doesn't even have the units of an area.

I'm only concerned with the triangle on the sides making 45 degrees angle.. because this is how the tributary areas of slabs were calculated which the beams adjacent to it are taking the load... by 45 degrees. In the formula of one of the trapezoidal area... this is the engineering formula for area of one trapezoidal

Lx/4 * (2- Lx/Ly) valid only for 45 degrees triangles.

I understood the Lx/4 part.. if the length of the small side is 4 meters. then each triangle is 1 meter. But the 2 - Lx/Ly I don't understand how it is derived.. but it works...

when you solve for Lx/4 * (2- Lx/Ly), you really get the area of the trapezoidal.. let's say the short side is 4 meters and long side is 12 meters.. then you have

Lx/4 * (2- Lx/Ly) = 4/4 * (2 - 4/12) = 1 * (2 - 0.3333) = 1 * 1.66667 = 1.6667

then multiply by 12 (long side) to get the area of the trapezoidal = 20 sq. m

Using the easier way to calculate one trapezoidal

Area of the rectangle is 4 x 12 = 48 - area of triangles = 48 - (4x4/4)*2 = 48 - 8 = 40 /2 = 20 sq. m

What's special about 2 - Lx/Ly early above.. why does the method produce the area of the trapezoidal too?

 

[mfb]

Ah, the 45 degree was the missing piece of information.

Then the triangles have an area of $\frac{L_x^2}{4}$ each - note the square.

What's special about 2 - Lx/Ly early above.. why does the method produce the area of the trapezoidal too?

Let's derive it: The total area is $L_x L_y$. We remove two triangles, so we have $L_x L_y - 2 \frac{L_x^2}{4}$ left. The two trapezoids have the same area so we just have to divide the result by 2: $A = \frac{L_x L_y}{2} - \frac{L_x^2}{4} = \frac{L_x L_y}{4} \left( 2-\frac{L_x}{L_y}\right)$ Your formula is missing one factor $L_y$.

 

[dahoa]

Ah, the 45 degree was the missing piece of information.

Then the triangles have an area of $\frac{L_x^2}{4}$ each - note the square.Let's derive it: The total area is $L_x L_y$. We remove two triangles, so we have $L_x L_y - 2 \frac{L_x^2}{4}$ left. The two trapezoids have the same area so we just have to divide the result by 2: $A = \frac{L_x L_y}{2} - \frac{L_x^2}{4} = \frac{L_x L_y}{4} \left( 2-\frac{L_x}{L_y}\right)$ Your formula is missing one factor $L_y$.

In slab load contribution to beam.. you don't use Ly.. you only multiply it later by Ly
So $A = \frac{L_x }{2} - \frac{L_x^2}{4} = \frac{L_x }{4} \left( 2-\frac{L_x}{L_y}\right)$

The unit of the above seems to be area per meter.. then only after you multiply by Ly do you get the total area of the trapezoidal...

What is the unit of this area per meter? or area contribution per meter? You need this so you can know the load contribution on the beam per meter.. I know the left and right side of the trapezoidal has smaller area..

 

[mfb]

In slab load contribution to beam.. you don't use Ly.. you only multiply it later by Ly

Then it is not an area. You could call it "area density", or "area per length", but it has the unit of a length, so something like "effective height" might be more useful.