element41$
- 7
- 0
Homework Statement
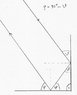
Two plane mirrors are joined along side at a right angle. Both are perpendicular to the table top, like walls meeting at a corner.
For a general angle of theta, determine the direction of the reflected ray which leaves the double mirror?
Homework Equations
n/a
The Attempt at a Solution
this is what i said:
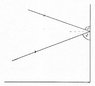
For a general angle of incidence theta the direction of the reflected ray which leaves the double mirror is the same as the angle that enters the double mirror. From the example given the light enters the double mirror on the left at a 45 degree angle. It then bounces off the mirror to the mirror at the right and reflects at a 45 degree angle from that mirror.
This is wrong though
Thank you