What is the Geometrical Proof for the Coordinate Transformation Formula?

[Karol]

Homework Statement

Prove:
$$\cos\alpha\cdot\cos\alpha'+\cos\beta\cdot\cos\beta'+\cos\gamma\cdot\cos \gamma'=\cos\theta$$
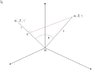
See drawing Snap1

Homework Equations

None

The Attempt at a Solution

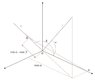
See drawing Snap2. i make the length of the lines 1 and 2 to equal one, for simplicity.
The projection of line 1 on one of the axes is cos(α).
$\cos\alpha\cdot\cos\beta$ is the projection of line OA=cos(α) on line 2, which causes line AB to be perpendicular to line 2.
If i will make the same procedure for all 3 axes and add the 3 projections on line 2 i have to get, see Snap1, line OC which is $1\cdot\cos\theta$, but i don't know how to do it.
The book from which i took this problem says i have to solve it from geometrical considerations.
Where can i find the proof to this problem?

 

[ehild]

You have two straight lines given with their direction cosines, and θ is the angle between the lines?

The direction cosines are the Cartesian components of the unit tangent vector of the line. $\vec e_1=<\cos(\alpha);\cos(\beta);\cos(\gamma)>$ and $\vec e_2=<\cos(\alpha');\cos(\beta');\cos(\gamma')>$. The dot product of the unit vectors $\vec e_1$ and $\vec e_2$ is $\vec e_1\cdot\vec e_2 =\cos(\alpha)\cos(\alpha')+\cos(\beta)\cos(\beta')+\cos(\gamma) \cos( \gamma ')$. How is the dot product related to the angle θ between the unit vectors?

ehild

 

[Karol]

Thanks, Ehild, the dot product is just that, the cos between the lines.