SUMMARY
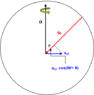
The discussion focuses on the derivation of the radial component of gravitational acceleration as presented in Taylor's "Classical Mechanics," specifically in Chapter 9. The key equations discussed are g = g_0 + Ω² * Rsinθρ and g_rad = g_0 - Ω² * Rsin²θ. Participants clarify the projection of the centrifugal force (FCF) on the gravitational vector, emphasizing the use of sine for the projection on the y-axis due to the angle θ being measured from the Earth's rotation axis. The radial component is confirmed as g_rad = g_0 - a_CF * sin(θ), where a_CF = Ω²Rsinθ.
PREREQUISITES
- Understanding of gravitational acceleration concepts
- Familiarity with vector projections in physics
- Knowledge of centripetal acceleration and its derivation
- Basic comprehension of coordinate systems in mechanics
NEXT STEPS
- Study Taylor's "Classical Mechanics" Chapter 9 for deeper insights into centrifugal acceleration
- Learn about vector projection techniques in physics
- Explore the derivation of centripetal acceleration in rotating systems
- Review coordinate transformations and their applications in mechanics
USEFUL FOR
Students of physics, educators teaching mechanics, and anyone interested in understanding gravitational forces in rotating reference frames.