What is the kinetic energy of a block as water pours out of a container?

[byahnoob]

Homework Statement

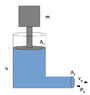
A block of mass m is connected to a massless rod and plunger of area A1 on a cylindric container of water. At

the bottom of the container there is a pipe that leads to an opening of area A2 where the water pours out at a

velocity v. The block starts at rest with the plunger a distance h from the bottom of the container.

A] What pressure does the block apply to the water? Only use A1 , m, and g in your answer.

B] What kinetic energy does the block have as water pours from the opening? Express your answer in terms of m, g, A1 , A2 , P0 , h, and ρ .

HINT* - solving for 1⁄2 v2 will get you very close to an expression for K.

[ATTACHED PICTURE OF PROBLEM]

Homework Equations

F = PA
Bernoulli's equation
KE = 1/2mv^2

The Attempt at a Solution

A] F = PA
mg = PA1

answer:
mg/A1 = P

B] Using Bernoulli's equation
P + pgh = P0 + 1/2pv^2
mg/A1 + pgh = P0 + 1/2pv^2

REARRANGE

(1/p)(mg/A1 + pgh + P0) = 1/2v^2

answer:
KE = 1/2mv^2 = (m/p)(mg/A1 + pgh + P0)
AM I CORRECT OR WRONG? I don't know how to get that A2 to the answer of part B

 

[haruspex]

There are two velocities here, which you need separate variables for: the velocity of the water from the outlet (the given v), and the velocity of the mass (for which you need another symbol) . There is a relationship between them.