maxsthekat
- 55
- 0
First off, thanks to alphysicist for helping with my last problem :) I'm not trying to flood the board, but I have given a good attempt to this problem and can't see where I'm going wrong. Thanks to the community for having this board in the first place-- you guys are great! :)
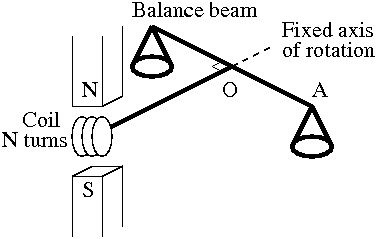
A small coil with N = 240 turns is mounted on one end of a balance beam and introduced between the poles of a magnet as shown in the figure. The cross-sectional area of the coil is 0.9 cm2 and the length of the arm OA of the balance beam is 31 cm. When there is no current in the coil, the beam is horizontal. On passing a current of 18 mA through the coil, the equilibrium is restored by putting a mass of 76 mg on the balance pan A. Find the magnetic field in the region of the coil.
Mechanical Torque = r x F = r*F*Sin(theta) where theta is the angle between r and F
F = force on object (in this case due to gravity) = mg
r = radius from pivot
Magnetic Torque = u x B = u*B*Sin(theta) where theta is the angle between u and B; u = magnetic dipole moment = n*I * A (turns * current * area vector)
Since the arm is in balance, we know that the magnitude of Magnetic torque = Mechanical Torque.
Therefore:
r x F = u x B
r*F*Sin(theta) = n*I*A*B*Sin(theta)
Sin(theta) in both cases = 1 (theta = 90 degrees)
r*F = n*I*A*B
r*m*g = n*I*A*B
B = (rmg) / (nIA)
Yet, this is incorrect. Does anyone have any hints you might be able to offer? Thanks again for your help!
Homework Statement
A small coil with N = 240 turns is mounted on one end of a balance beam and introduced between the poles of a magnet as shown in the figure. The cross-sectional area of the coil is 0.9 cm2 and the length of the arm OA of the balance beam is 31 cm. When there is no current in the coil, the beam is horizontal. On passing a current of 18 mA through the coil, the equilibrium is restored by putting a mass of 76 mg on the balance pan A. Find the magnetic field in the region of the coil.
Homework Equations
Mechanical Torque = r x F = r*F*Sin(theta) where theta is the angle between r and F
F = force on object (in this case due to gravity) = mg
r = radius from pivot
Magnetic Torque = u x B = u*B*Sin(theta) where theta is the angle between u and B; u = magnetic dipole moment = n*I * A (turns * current * area vector)
The Attempt at a Solution
Since the arm is in balance, we know that the magnitude of Magnetic torque = Mechanical Torque.
Therefore:
r x F = u x B
r*F*Sin(theta) = n*I*A*B*Sin(theta)
Sin(theta) in both cases = 1 (theta = 90 degrees)
r*F = n*I*A*B
r*m*g = n*I*A*B
B = (rmg) / (nIA)
Yet, this is incorrect. Does anyone have any hints you might be able to offer? Thanks again for your help!
Last edited: