What is the mass moment of inertia?

[PrincessIceFall]

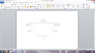
What is the mass moment of inertia about the longitudinal axis of the shape attached in this thread, but in 3 D?

I found this "Handbook of Equation for Mass and Area Properties of Various Geometrical Shapes" which gives the mass moment of inertia of a regular octagon. I initially thought that I will use that same equation and simply divide it by 2. However, I realized a couple of issues:

1. The equation given is for a 2D shape, and I need an equation for a 3D shape
2. The shape that I have attached with this thread, is not purely half an octagon, as for an octagon, all the sides are equal, and in this shape all of the sides are not equal (Please see the attachment)
3. I need the mass moment of inertia about the longitudinal axis only

So yeah, this is not easy as there is no equation available online that applies to what I want. Can anyone help me? Do you have any idea how I can find the mass moment of inertia for this shape in 3D? Thank you

 

[SteamKing]

Well, we have some questions in turn for you:
1. The shape shown is only 2-D. What 3-D shape do you desire to calculate the mass moment of inertia? (that is, is the missing dimension a thickness which comes out of the plane of view?
2. What axis is the longitudinal axis?
3. Does this figure have any dimensions?
4. What material is the figure made from?

 

[PrincessIceFall]

Well, we have some questions in turn for you:
1. The shape shown is only 2-D. What 3-D shape do you desire to calculate the mass moment of inertia? (that is, is the missing dimension a thickness which comes out of the plane of view?
2. What axis is the longitudinal axis?
3. Does this figure have any dimensions?
4. What material is the figure made from?

1. Yes, the shape shown is in 2 D, because I could not draw the 3 D shape in ms-word. The 3 D shape would be a prism of the drawn shape. So basically, it would be what the drawn shape would look like if it was extruded to a length of say 'L'
2. Longitudinal axis is the axis from the centroid of the body that points out of the page/screen toward you. I guess you could say that its the z-axis. But in some textbooks they call the longitudinal axis as the x-axis.
3. The shape could have any dimensions. Which is why I have denoted them with letters.
4. Does the material matter? I mean I just want the mass moment of inertia 'equation' for the 3 D shape because the material (just like the dimensions) could be anything.

I hope these answer your questions, and if you have any further question please let me know.

 

[SteamKing]

1. Yes, the shape shown is in 2 D, because I could not draw the 3 D shape in ms-word. The 3 D shape would be a prism of the drawn shape. So basically, it would be what the drawn shape would look like if it was extruded to a length of say 'L'
2. Longitudinal axis is the axis from the centroid of the body that points out of the page/screen toward you. I guess you could say that its the z-axis. But in some textbooks they call the longitudinal axis as the x-axis.
3. The shape could have any dimensions. Which is why I have denoted them with letters.
4. Does the material matter? I mean I just want the mass moment of inertia 'equation' for the 3 D shape because the material (just like the dimensions) could be anything.

I hope these answer your questions, and if you have any further question please let me know.

Yes, the material matters. You need this information to put the mass in the mass moment of inertia.

Taking the z-axis as the longitudinal axis, and using a centroidal origin for the coordinate system, the mass moment of inertia I_zz for the body will be:

I_zz = ∫∫∫ (x² + y²) ⋅ dM, where dM = ρ dV = ρ dx dy dz for an homogenous body of mass density ρ.

Since the body is a prism in the z-direction, some simplifications can be made to the integral for I_zz:

I_zz = ∫∫∫ (x² + y²) ⋅ dM = ∫∫∫ (x² + y²) ⋅ ρ dx dy dz =

ρ ⋅ ∫ [∫∫ (x² + y²) dx dy] dz = ρ ⋅ z ⋅ ∫∫ x² dA + ρ ⋅ z ⋅ ∫∫ y² dA

The integrals ∫∫ x² dA and ∫∫ y² dA are simply the second moments of the area of the cross section of the prism about the y and x axes, respectively.

Since the cross section of the prism is a polygon, the second moments of area can be calculated using only the coordinates of the vertices of the polygon.

This method can be derived from Green's Theorem in the plane by which a closed curve described by piecewise line segments can have its area and first and second moments of area calculated by using only the (x,y) coordinates of the endpoints of the line segments as input.

See this article, p. 8, for the formulas: http://www.infogoaround.org/JBook/CentroidInertia.pdf

The curve is described starting at an arbitrary endpoint of one of the line segments and proceeding counterclockwise around the area of interest until reaching the starting point. Counterclockwise orientation produces positive areas and moments while clockwise orientation produces negative areas and moments, so that polygons with holes can also be handled by this method.

The areas and moments are referenced about the coordinate axes. The parallel axis theorem is required to determine centroidal values of these quantities once you have completed the circuit of the polygon, if the coordinates of the vertices of the polygon are not referenced to the centroid of the cross section.

This method can be employed on simple polygons, like squares and rectangles, and these figures can be used as a check on your calculations.

 

[PrincessIceFall]

Yes, the material matters. You need this information to put the mass in the mass moment of inertia.

Taking the z-axis as the longitudinal axis, and using a centroidal origin for the coordinate system, the mass moment of inertia I_zz for the body will be:

I_zz = ∫∫∫ (x² + y²) ⋅ dM, where dM = ρ dV = ρ dx dy dz for an homogenous body of mass density ρ.

Since the body is a prism in the z-direction, some simplifications can be made to the integral for I_zz:

I_zz = ∫∫∫ (x² + y²) ⋅ dM = ∫∫∫ (x² + y²) ⋅ ρ dx dy dz =

ρ ⋅ ∫ [∫∫ (x² + y²) dx dy] dz = ρ ⋅ z ⋅ ∫∫ x² dA + ρ ⋅ z ⋅ ∫∫ y² dA

The integrals ∫∫ x² dA and ∫∫ y² dA are simply the second moments of the area of the cross section of the prism about the y and x axes, respectively.

Since the cross section of the prism is a polygon, the second moments of area can be calculated using only the coordinates of the vertices of the polygon.

This method can be derived from Green's Theorem in the plane by which a closed curve described by piecewise line segments can have its area and first and second moments of area calculated by using only the (x,y) coordinates of the endpoints of the line segments as input.

See this article, p. 8, for the formulas: http://www.infogoaround.org/JBook/CentroidInertia.pdf

The curve is described starting at an arbitrary endpoint of one of the line segments and proceeding counterclockwise around the area of interest until reaching the starting point. Counterclockwise orientation produces positive areas and moments while clockwise orientation produces negative areas and moments, so that polygons with holes can also be handled by this method.

The areas and moments are referenced about the coordinate axes. The parallel axis theorem is required to determine centroidal values of these quantities once you have completed the circuit of the polygon, if the coordinates of the vertices of the polygon are not referenced to the centroid of the cross section.

This method can be employed on simple polygons, like squares and rectangles, and these figures can be used as a check on your calculations.

The cross section of the prism is not a polygon, since all the sides are not equal

 

[SteamKing]

The cross section of the prism is not a polygon, since all the sides are not equal

A general polygon can be any figure which is closed and whose sides are composed of straight line segments.

A regular polygon is a special kind of polygon in which all the sides are of equal length, and all internal angles between the sides are equal.

http://en.wikipedia.org/wiki/Polygon

The method of calculation for the MOI of polygons discussed in previous posts is not limited to regular polygons.