- #1
mhayer7
- 3
- 0
What is the maximum mass of rocks one can lift using a wheelbarrow PLEASE HELP!
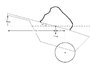
A man is using a wheelbarrow to transport rocks across the garden. The man can generate a maximal vertical force of 500N to lift the wheelbarrow. If the centre of mass of the rocks is .25m horizontally from the wheel, and the handle of the wheelbarrow is 1.5m at an angle of 35 degress from the horizontal, what is the maximum mass of rocks he can lift?
sum or torques equation. f=ma, phythagorean theorem.
I tried drawing a diagram for this but ended up confusing myself. I know i need to use similar triangles to try and find the max weight since we have the force applied by the man but am not sure how to do it. I know it will be something like MASS OF ROCKS TIMES GRAVITY X .25M = 500N TIMES 1.5M. But I am very confused as to how to accomplish this. Any help is appreciated!
Homework Statement
A man is using a wheelbarrow to transport rocks across the garden. The man can generate a maximal vertical force of 500N to lift the wheelbarrow. If the centre of mass of the rocks is .25m horizontally from the wheel, and the handle of the wheelbarrow is 1.5m at an angle of 35 degress from the horizontal, what is the maximum mass of rocks he can lift?
Homework Equations
sum or torques equation. f=ma, phythagorean theorem.
The Attempt at a Solution
I tried drawing a diagram for this but ended up confusing myself. I know i need to use similar triangles to try and find the max weight since we have the force applied by the man but am not sure how to do it. I know it will be something like MASS OF ROCKS TIMES GRAVITY X .25M = 500N TIMES 1.5M. But I am very confused as to how to accomplish this. Any help is appreciated!