Jiho
- 20
- 4
Hello.
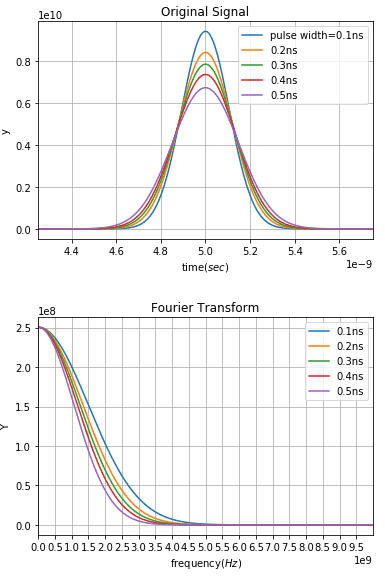
So I confused what is the Nyquist frequency at Gaussian signal. I need to know Nyquist frequency for Fourier analysis, but alll of the Gaussian signal's critical frequcny is 0hertz.
I'm studying Fourier analysis. If we look at attached graph where Gaussian functions are transformed by Fourier analysis, we can find Gaussian functions in frequency domain have maximum value at 0 hertz. So I confused what is the Nyquist frequency at Gaussian signal. I need to know Nyquist frequency for Fourier analysis, but alll of the Gaussian signal's critical frequcny is 0hertz.
