- #1
What is the meaning of Ai Aii Bi Bii in Vector potential?
- Thread starter garylau
- Start date
In summary: There are many different paths that correspond to the "outward" closed surface integral are equal to 0.
- #2
phyzguy
Science Advisor
- 5,227
- 2,276
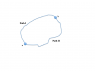
The notations I and II are intended to indicate two different paths from a to b, as in the attached drawing. So the difference between the integral along path I and the integral along path II is equal to the integral along path I plus the integral along path II in the other direction, which is the integral around the whole loop, which is zero.
Attachments
- #3
Nugatory
Mentor
- 15,132
- 9,899
The I and II indicate that the line integrals are being taken along two different paths between a and b.garylau said:
[Edit: like phyzguy just said a moment before me]
- #4
- 5,737
- 2,989
Griffths is taking two different paths (I) and (II) in a path integral from point "a" to point "b". He first does a loop (going from "a" to "b" by path 1 and then going from "b" to "a" by path 2) by putting a "-" sign on it. (Notice the position of the endpoints in the integral.) ...edit .. I see 2 very equivalent responses came in right before me.
- #5
garylau
- 70
- 3
itphyzguy said:
But it sound unreasonable he gives the proof like thisin fact the equation on the left side are equal to the right sidephyzguy said:
(1)+(11)(A->B) =(1)-(11)(B->A) ?
What is Griffith trying to doing in the equation
- #6
- 5,737
- 2,989
(I)A=>B-(II)A=>B=(I)A=>B+(II)B=>A=0 so that (I)A=>B=(II)A=>B is what he is proving.(Hopefully you can distinguish between the actual equal signs and the equal signs that I used as part of an arrow from A to B.)garylau said:
- #7
garylau
- 70
- 3
Charles Link said:
Oh i See thank you
- #8
garylau
- 70
- 3
There is one more question i want to askCharles Link said:
Why the surface integral(II) is inward in this case?
because there are only two possibility for a closed surface integral?
but i think there can are many different paths which correspond to the "outward" closed surface integral are equal to 0
So the proof is not general?
Attachments
- #9
- 5,737
- 2,989
The proof is quite general. The integrals are line integrals, not surface integrals.
FAQ: What is the meaning of Ai Aii Bi Bii in Vector potential?
What is the definition of Ai Aii Bi Bii in Vector potential?
Ai Aii Bi Bii is a mathematical notation used to represent the components of a vector potential. The vector potential is a vector field in three-dimensional space that is used to describe the magnetic field in classical electromagnetism.
Why is Ai Aii Bi Bii used in vector potential?
Using Ai Aii Bi Bii notation allows for a more concise and organized representation of the vector potential. It also makes it easier to perform calculations and manipulate equations involving the vector potential.
How is Ai Aii Bi Bii related to the magnetic field?
The vector potential, represented by Ai Aii Bi Bii, is related to the magnetic field through the equation B = ∇ x A, where B is the magnetic field and A is the vector potential. This equation is known as the Biot-Savart law.
Can Ai Aii Bi Bii be used to describe other vector fields?
Yes, Ai Aii Bi Bii notation can be used to represent components of any vector field in three-dimensional space. However, it is most commonly used to describe the vector potential in classical electromagnetism.
How is Ai Aii Bi Bii different from other notations used in vector calculus?
Ai Aii Bi Bii notation is different in that it specifically represents the components of the vector potential. Other notations, such as Cartesian coordinates or spherical coordinates, can also be used to represent vector fields, but they may not be as efficient or organized as Ai Aii Bi Bii notation for describing the vector potential.