sami23
- 69
- 1
Homework Statement
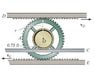
The wheel is rigidly attached to gear A, which is in mesh with gear racks D and E. If D has a velocity of v_D = 5 ft/s to the right and wheel rolls on track C without slipping, determine the speed of gear rack E. Set r = 1.4 ft.
Homework Equations
angular velocity of gear \omega= v_D / r_D/IC
v_E = \omega * r_E/IC
where r_D/IC = (1.4 + 0.75) = 2.15 ft
and r_E/IC = 0.75 ft
The Attempt at a Solution
\omega = 5 / 2.15 = 2.3256 rad/s
v_E = 2.3256 * 0.75 = 1.744 ft/s to the left but it's wrong
What did I do wrong? Please help