What is the Moment of Inertia of the Pulley?

[GreenPrint]

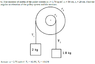
Homework Statement

See first attachment

Homework Equations

The Attempt at a Solution

a = r * alpha
r = a / alpha

If I think of the whole pulley as a system...

Ʃ F_sys = m_sys*a = Fg_1 - Fg_2

I called the 2 kg block, block 1, I called the 1.8 kg block block 2.

a = [ Fg_1 - Fg_2 ] / m_sys
a = [ m_1 * g - m_2 * g ] / [ m_1 + m_2 ]
a = [ g ( m_1 - m_2) ] / [ m_1 + m_2 ]

putting this into
r = a / alpha
r = [ g ( m_1 - m_2) ] / [ alpha ( m_1 + m_2 ) ]

putting in values (I used the given answer for alpha just to see what the radius was)

r = [ 9.8 ( 2 - 1.8 ) ] / [ 2.76 ( 2 + 1.8 ) ] ≈ .187 m

I was wondering what radius is this exactly?

 

[gneill]

For this problem you need to work with both linear and angular methods; In your attempt so far you haven't accounted for the moment of inertia of the pulley system.

Hints:
Draw FBD's for the two masses and write expressions for their accelerations in terms of the (currently unknown) tensions in the strings attached to them.

Relate these tensions to torques on the pulley system. What angular acceleration will result?

Ponder a while on the relationships between the accelerations in the two strings and the angular acceleration of the pulleys

 

[GreenPrint]

So is
r ≈ .187 m
a meaningless quantity?

 

[GreenPrint]

Well I have these three equations
2 * a_1 = 19.6 - T_1
1.8 * a_2 = 17.64
1.70 * alpha = .5 * T_1 - .2 * T_2

I established this from free body diagrams and
Ʃ t = I*alpha

 

[GreenPrint]

hmm i think i got it

 

[GreenPrint]

but what is the radius that i found earlier?

 

[gneill]

but what is the radius that i found earlier?

Since it doesn't correspond to the physical system as it is portrayed in the problem, it doesn't have a 'meaning' in that context.

 

[GreenPrint]

Since it doesn't correspond to the physical system as it is portrayed in the problem, it doesn't have a 'meaning' in that context.

Hm... interesting... is there a way to write the net force on the system as a whole ignoring the tensions then?

 

[gneill]

Hm... interesting... is there a way to write the net force on the system as a whole ignoring the tensions then?

What do you mean by the 'net force on the system'? The net torque being applied to the pulley system?

If the system was static (not moving, not rotating) then yes, you could claim that the tensions in the strings are determined entirely by gravity acting on the hanging masses.

When the system is in accelerated motion, however, the tensions also depend upon the inertial forces so introduced. This includes the inertia of the masses themselves and of the pulley.

 

[GreenPrint]

Like let's say we had the same situation except the blocks were just sitting on a pulley at the same radius and the pulley had no friction and we ignored the rotational motion. We could say that

Ʃ F_sys = m_sys * a = Fg_1 - Fg_2
and just ignore the tension from the string completely
and solve for acceleration
a = [ g ( m_1 - m_2 ) ] / [ m_1 + m_2 ]

I was wondering if such a similar thing could be done when we don't ignore the rotational motion.

 

[gneill]

Like let's say we had the same situation except the blocks were just sitting on a pulley at the same radius and the pulley had no friction and we ignored the rotational motion. We could say that

Ʃ F_sys = m_sys * a = Fg_1 - Fg_2
and just ignore the tension from the string completely
and solve for acceleration
a = [ g ( m_1 - m_2 ) ] / [ m_1 + m_2 ]

I was wondering if such a similar thing could be done when we don't ignore the rotational motion.

Nope. It's like trying to ignore a significant third mass in your example.

 

[GreenPrint]

ahh the mass of the pulley?
so if the mass of the pulley is not given and we can solve for the acceleration we can solve for the mass of the pulley?

 

[gneill]

ahh the mass of the pulley?
so if the mass of the pulley is not given and we can solve for the acceleration we can solve for the mass of the pulley?

You're given the moment of inertia of the pulley. This is the angular equivalent to mass.