mathman2
- 5
- 0
View attachment 3492
I really need help creating an optimization problem for this, I have this so far..
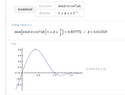
I(φ, φMax) = Sin(φ * π/φMax)/(Sin(x)2 + 1)
With that said, I don't really understand how to enter values into that equation, "Phi" is really throwing me off, is it a constant or should I treat it as a variable like "theta"??
I really need help creating an optimization problem for this, I have this so far..
I(φ, φMax) = Sin(φ * π/φMax)/(Sin(x)2 + 1)
With that said, I don't really understand how to enter values into that equation, "Phi" is really throwing me off, is it a constant or should I treat it as a variable like "theta"??