WhiteWolf98
- 89
- 8
Homework Statement
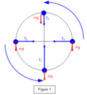
A ##5 ~kg## mass performs circular motion at the end of a light, inextensible string of length ##3~m##. If the speed of the mass is ##2 ~ms^{-1} ## when the string is horizontal, what is its speed at the bottom of the circle?
(assume ##g=10~ms^{-1}##) (Ans: ##8~ms^{-1}##)
I'm not sure in what plane? as such, to imagine this question. I know the equations for a horizontal and vertical circle, as well as a conical pendulum, but the question just doesn't make sense to me. Any help would be appreciated. Thank you