warfreak131
- 186
- 0
Homework Statement
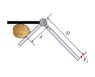
The nut is now placed in a nutcracker with only one lever, as shown, (Intro 3 figure) and again friction keeps the nut from slipping. The top "jaw" (in black) is fixed to a stationary frame so that a person just has to apply a force to the bottom lever. Assume that F_2 is directed perpendicular to the handle.
Homework Equations
\Sigma\tau=0
The Attempt at a Solution
I'm not sure if the sum of the torques includes F_{2}D and/or F_{2}d. I though that it was the sum of the torque of the smaller handle + the torque of the larger handle + the normal force. Since counter clockwise is positive, it would be \tau_{nut}-\tau_{small}-\tau_{large}=0 and solve for F_{2}, but that's not right.