lendav_rott
- 232
- 10
Homework Statement
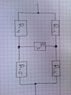
Attached diagram. The resistors don't have any concrete resistances.
Need to express the total resistance of the part of the circuit shown in the picture.
Homework Equations
Series - R= ƩRn
Parallel - R = (ƩRn-1)-1
The Attempt at a Solution
R1 and R2 make a series - so the resistance of it would be R1+R2 and same with R4+R5.
And using that approach I would have 3 parallel connections.
R1+R2
R3
R4+R5
And compute the total resistance with the parallel formula...but, something just doesn't feel right.