geniusno.198
- 4
- 0
Homework Statement
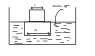
Two cubes made of the same material and edge length 'a' and '2a'. They are placed in a liquid of density σ such that the larger cube is completely submerged when the smaller cube is placed on top of it and the lower surface of smaller cube is just touching the surface of the liquid.
Now, if the smaller cube is heated sucjh that it melts uniformly and very slowly (reducing all dimensions simultaneously) such that the edge reduces at a constant rate α then the velocity of the larger cube as a function of time will be (assuming molten material evaporates immediately).
Homework Equations
let the densities of both the blocks be 'ρ'
Mass of the larger block= 8ρa^3 (mass=volume*density)
Mass of smaller block= ρa^3
since weight of both the blocks is balanced by the buoyant force the weight of both the blocks together is equal to the buoyant force.
(ρa^3+8ρa^3)g = Volume of body submerged*density of liquid*g
=8ρa^38σg
therefore ρ=8σ/9
The Attempt at a Solution
I thought what we basically have to find is the rate at which the mass of the small block is changing. so we we have to find the differential of the mass of the smaller block with respect to time. therefore d(8σa^3/9)/dt = 8σa^2/3 8 da/dt. but according to the question da/dt=α. I got stuck here,I don't know what I should do next.