RIT_Rich
A small solid marble of mass m and radius r will roll without slipping along the loop-the-loop track shown in Fig. 12-34 if it is released from rest somewhere on the straight section of track. For the following answers use m for the mass, r for the radius of the marble, R for the radius of the loop-the-loop and g for the acceleration due to gravity.
Here's the picture:
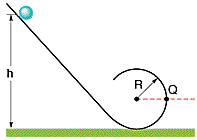
a) a) From what minimum height h above the bottom of the track must the marble be released to ensure that it does not leave the track at the top of the loop? (The radius of the loop-the-loop is R. Assume R>>r.)
Can anyone give me any hints as to how to do this problem, becasue to tell you the truth I don't even know how to start it.
Thanks a lot
Here's the picture:
a) a) From what minimum height h above the bottom of the track must the marble be released to ensure that it does not leave the track at the top of the loop? (The radius of the loop-the-loop is R. Assume R>>r.)
Can anyone give me any hints as to how to do this problem, becasue to tell you the truth I don't even know how to start it.
Thanks a lot
