charlie05
- 128
- 6
Homework Statement
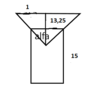
The astronomer fell into the well. The well is circular, depth H = 15m, radius r = 1m. The astronomer has eyes at h = 1.75m. Observation is from the well axis, refraction is neglected.
How many % of sky can an astronomer see at one time?
How many % of sky can an astronomer see during the whole year?
Homework Equations
sine theorem, cosine theorem od sides and angles
The Attempt at a Solution
tg alfa=1/13,25...alfa=0,0013°.
2D well viev...2*alfa=0,0026°
but view is 3D...have I use solid angle? normally an astronomer could see 2π?
Attachments
Last edited: