What space contracts in Special Relativity?

[dubiousraves]

Hi. I know that space for an object in motion will contract, relative to an observer. We generally read that space contracts for the object in the direction of motion. But doesn't space around the object also contract? Can someone clarify this? Thanks.

 

[dEdt]

I know that space for an object in motion will contract, relative to an observer.

I don't think this is a good way of thinking about length contraction.

According to the theory of relativity, the length of an object in motion (along the direction of motion) is shorter than if the object was at rest. This is least ambiguous way of describing length contraction.

The problem with characterizing length contraction as a contraction of space itself is that space doesn't contract. Space is always defined relative to an observer. Suppose someone named Alice is observing an object. If that object starts moving, Alice's description of space doesn't change at all. Rather, the object just shrinks.

 

[HallsofIvy]

Hendrik Lorentz, for whom the Lorentz transforms are named, had a theory that would explain the contraction of a moving object- since the magnetic field of a charged object was NOT invariant under motion, he suggested that in some, as yet unknown, way, the magnetic field in a moving object was stronger in the direction of motion and so caused it to contract. That would cause a material object to contract, not the space around it. But later experiment (in particular the "Kennedy experiment" which was like the Michaelson-Morley experiment but with arms of differing length, showed that this is not true. Contrary to what dEdts says, if you have two poles, one after the other, moving in the direction of their lengths, the space between them also contracts. "Length contraction" is a contraction of space, not just material objects.

 

[dubiousraves]

OK thanks. Actually, I meant to say "length" contraction. But let's take the example of a rocket making a round trip to a nearby star at close to c. According to the rocket's clocks, maybe 50 years pass (I'm not doing math here, just giving a rough estimate), but back on Earth thousands of years have elapsed. My question is, in the length-contraction part of this journey, what exactly is seen as contracting? Obviously, it can't just be the rocket shrinking that causes all the duration difference, so I'm assuming that the lengths of space are also contracting. Or, is it just that the vast majority of the difference is due to time dilation? Thanks. Feel free to give a formula for the length contraction.

 

[dubiousraves]

Ah, thanks Hallsoflvy, I didn't see your comment until after I posted my response above. I would still like to see the formula(s) that delineate which lengths/spaces are contracting and in what proportion these are to the time dilation.

 

[dEdt]

HallsofIvy

Two points:
1) It's a fact that the intermolecular forces in a moving object are different than in a stationary object. Fitzgerald used this observation to predict length contraction. There's no reason to think that his derivation or reasoning were wrong, considering that he used Maxwell's equations to get his result and Maxwell's equations are Lorentz invariant.

2) If you have two poles separated by some distance, how the distance changes with time depends on how exactly you accelerate the two poles. It's possible to accelerate them so that the distance grows, shrinks, or stays the same.

dubiousraves

Let's analyze the rocket trip from two reference frames: the Earth's and the rocket's.

From the Earth's reference frame, the only thing that's shrinking is the rocket. The distance to the star does not change in the slightest. From the perspective of someone on Earth, the reason that the astronauts on the rocket think the trip only took 50 years is time dilation.

According to the theory of relativity, if a process at rest takes a time $T$ to complete, then the same process moving with speed $v$ will take a longer time to complete, namely $\frac{T}{\sqrt{1-v^2/c^2}}$. This is known as time dilation, and explains why the astronauts would only think that 50 years elapsed: their clocks were slowed down!

From the astronaut's reference frame, it's the Earth and the star that are moving. Hence the distance between them contracts, which makes the journey that much shorter. That's the reason, from the astronaut's perspective, why the trip only took 50 years.

 

[dubiousraves]

Thanks. I am aware of the time dilation equation. However, if you say the distance between the Earth and the star contracts from the astronaut's reference frame, is there not a formula that would express that exact contraction?

 

[ghwellsjr]

Thanks. I am aware of the time dilation equation. However, if you say the distance between the Earth and the star contracts from the astronaut's reference frame, is there not a formula that would express that exact contraction?

The formula for Length Contraction is the inverse of the one for Time Dilation, but those are just short-cuts that can get you into trouble. The equations that will never get you into trouble are called the Lorentz Transformation process. I like to use units for a simplified version of those equations where c has the value of 1, for example, 1 foot per nanosecond. I also like to express velocity as a fraction of c which we call beta and assign the Greek letter beta (β).

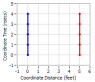
So let's say we have a rod of length 5 feet laying motionless along the x-axis. A spacetime diagram showing this simple scenario is:

The blue and red lines represent the two ends of the rod. The rod is spread out all along the space between it's two endpoints but we don't care about that, we only care about the endpoints that are used in determining its length. I'm only showing the positions of the endpoints for just a short time but we understand that the lines really extend upward and downward. Now let's see what happens if we transform the coordindates of this scenario into one that is moving at 0.6 toward the left. In this new diagram, the rod will be moving to the right at 0.6c and we can see how long it is.

The first thing we have to do when using the Lorentz Transformation is calculate the value of gamma, the Lorentz factor (the same value used to determine Time Dilation), as a function of β, in this case -0.6:

γ = 1/√(1-β²) = 1/√(1-(-0.6)²) = 1/√(1-0.36) = 1/√(0.64) = 1/0.8 = 1.25

Now we take the value of the t and x coordinates of each event (dot) in the diagram and calculate new values for the new diagram. The two equations for the new primed values are:

t' = γ(t-βx)
x' = γ(x-βt)

We can take another shortcut and just calculate the two endpoints of each of the two worldlines and fill in the extra events (dots) proportionally. So for the top of the blue line, x=0 and t=4:

t' = 1.25(4-(-0.6)*0) = 1.25(4) = 5
x' = 1.25(0-(-0.6)*4) = 1.25(2.4) = 3

For the bottom end of the blue line we have x=0 and t=0:

t' = 1.25(0-(-0.6)*0) = 1.25(0) = 0
x' = 1.25(0-(-0.6)*0) = 1.25(0) = 0

For the top of the red line we have x=5 and t=4:

t' = 1.25(4-(-0.6)*5) = 1.25(4+3) = 1.25(7) = 8.75
x' = 1.25(5-(-0.6)*4) = 1.25(5+2.4) = 1.25(7.4) = 9.25

For the bottom of the red line we have x=5 and t=0:

t' = 1.25(0-(-0.6)*5) = 1.25(3) = 3.75
x' = 1.25(5-(-0.6)*0) = 1.25(5) = 6.25

From those calculations and by interpolating (or by more calculations) we can make this diagram:

Now it's important to know that when we want to determine the length of an object (or the space between objects), we have to do it along a line where time is constant. So look at the horizontal grid line where time is 5 nanoseconds. The top of the blue line is on that grid line at x=3 feet and immediately to its right is the second dot up on the red line with an x coordinate value of 7 feet. The difference between these to events (dots) is 4 feet. This is the contracted length of the rod from its Proper Length in its rest frame divided by gamma (5/1.25=4).

You can also see the Time Dilation in this diagram where the dots representing 1 nsec intervals of time in the rest frame of the rod are now stretched out to 1.25 nsec of Coordinate Time.

The other important feature of Special Relativity call Relativity of Simultaneity is also shown where events that were simultaneous in the first frame occur at different times in the transformed frame.

 

[Bill_K]

1) It's a fact that the intermolecular forces in a moving object are different than in a stationary object. Fitzgerald used this observation to predict length contraction. There's no reason to think that his derivation or reasoning were wrong, considering that he used Maxwell's equations to get his result and Maxwell's equations are Lorentz invariant.

He didn't have the slightest idea what he was doing, pure guesswork. Working in 1890, Lorentz knew nothing of Quantum Mechanics or the nature of intermolecular forces or what actually determines the size of an object.

 

[dubiousraves]

Thanks for that elegant explanation, GHWellsJr., but I'm still wondering if the the space AROUND a moving objects contracts.

 

[nitsuj]

Thanks for that elegant explanation, GHWellsJr., but I'm still wondering if the the space AROUND a moving objects contracts.

Is space itself ever measured? Or is it the length between points

 

[dEdt]

He didn't have the slightest idea what he was doing, pure guesswork. Working in 1890, Lorentz knew nothing of Quantum Mechanics or the nature of intermolecular forces or what actually determines the size of an object.

I don't think that's fair. True, his derivation was based on a simplified and classical model, but so was all of 19th century physics. Do we begrudge Clausius and Maxwell of their kinetic theory of gases because it used a simplified and classical model?

 

[Bill_K]

True, his derivation was based on a simplified and classical model

There is no such model, and Lorentz did not pretend to have one. You can't build a solid object out of Maxwell's Equations.

Do we begrudge Clausius and Maxwell of their kinetic theory of gases because it used a simplified and classical model?

How would you explain in classical terms the Lorentz contraction of a gas?

 

[ghwellsjr]

Thanks for that elegant explanation, GHWellsJr., but I'm still wondering if the the space AROUND a moving objects contracts.

I did try to hint at that when I said, "...when we want to determine the length of an object (or the space between objects)...", so the answer is yes. The blue and red lines can represent either the two ends of a single object or two separate objects, it doesn't matter.

But remember, length (or distance) contraction is merely a coordinate effect. When we change reference frames and use the Lorentz Transformation process, the time and length (or distance) coordinates change. Nothing has actually changed to the objects or the space. The same can be said for Time Dilation.

Observers in a scenario cannot tell that we switched to a different reference frame when we did the above exercise and so nothing changes either in what they see, what they measure, or what they observe. In fact, Length Contraction and Time Dilation are completely unobserverable. They can only be determined by observers by proactively sending out radar signals, waiting for their echoes, observing clocks on other objects, logging all the data and the times they occurred according to their own clock and then doing a lot of computation. Only after the entire scenario is over will they be able to go back and make diagrams like I did and see those coordinate effects.

 

[dEdt]

If you assume that intermolecular forces are electrical in nature then you can deduce, based on how the electric field of a moving point charge compares to a stationary charge, that the size of molecules as well as the intermolecular distance will shrink by a factor of gamma. I won't pretend that this is a precise derivation or anything (and as you mention, a precise derivation is classically impossible because classical physics does not permit the existence of solid bodies), but nonetheless my original point sill stands: contrary to what HallsofIvy stated, the contraction of a moving body is ultimately due to the behavior of the forces holding that body together, whether or not it's practically feasible to calculate length contraction by analyzing these forces. Special relativity doesn't change this fact. It only allows us to efficiently calculate what the length contraction will be without having to analyze, say, intermolecular forces.

As for the length contraction of a box of gas, the explanation is the same as for a rod: the box containing the gas will contract because of the behavior of the forces holding the box together.

 

[Mentz114]

If you assume that intermolecular forces are electrical in nature then you can deduce, based on how the electric field of a moving point charge compares to a stationary charge, that the size of molecules as well as the intermolecular distance will shrink by a factor of gamma. I won't pretend that this is a precise derivation or anything (and as you mention, a precise derivation is classically impossible because classical physics does not permit the existence of solid bodies), but nonetheless my original point sill stands: contrary to what HallsofIvy stated, the contraction of a moving body is ultimately due to the behavior of the forces holding that body together, whether or not it's practically feasible to calculate length contraction by analyzing these forces. Special relativity doesn't change this fact. It only allows us to efficiently calculate what the length contraction will be without having to analyze, say, intermolecular forces.

As for the length contraction of a box of gas, the explanation is the same as for a rod: the box containing the gas will contract because of the behavior of the forces holding the box together.

This is wrong. Molecular forces don't come into it. As ghwells said

But remember, length (or distance) contraction is merely a coordinate effect. When we change reference frames and use the Lorentz Transformation process, the time and length (or distance) coordinates change. Nothing has actually changed to the objects or the space. The same can be said for Time Dilation.

 

[WannabeNewton]

As for the length contraction of a box of gas, the explanation is the same as for a rod: the box containing the gas will contract because of the behavior of the forces holding the box together.

This entire discussion is going to lead down a road that has already seen blow after blow after blow in the past. Some people try to separate length contraction into two classes: the Lorentz contraction obtained from boosting between inertial frames, which these people would label a "coordinate artifact" and the Lorentz-Fitzgerald contraction which is what you are referring to and which said people would label a "real effect". Therefore these people would qualify Lorentz contraction as a different phenomenon from Lorentz-Fitzgerald contraction. Others would argue that they are not different phenomena but rather just different "components" of the length contraction relativized to a given observer (which is, IMO, the better viewpoint). With that terminological issue out of the way, it should be clear now that neither your posts nor those of others in this thread have encompassed both "components" of length contraction. Everyone is speaking past one another by exclusively referring to one or the other.

An analysis of the Ehrenfest paradox should help your conceptual understanding of the bridging of the two.

 

[JVNY]

This entire discussion is going to lead down a road that has already seen blow after blow after blow in the past. . .

At the risk of bringing blows down upon myself, can I ask some questions to clarify the two views?

Consider the basic barn and pole paradox, where the barn has a front door and a solid rear wall. A pole has greater proper length than the proper length of the barn; the pole and barn are in inertial motion with respect to each other; in the barn frame, the pole is length contracted and enters the barn through the front door; the door closes, and the pole is entirely within the barn (at least for a very short period of time in the barn frame).

dEdt and ghwellsjr, do you each agree that the pole is entirely within the barn in the barn frame for at least a short period of barn time?

dEdt: if yes, does this occur only if the rod is in absolute motion (such that its molecules are contracted due to the behavior of the forces holding the rod together), or do you conclude that there is a behavior of forces on the rod regardless of whether the rod had been accelerated, the barn had been accelerated, or even if one does not know which one was accelerated (given that we are told that there is no absolute motion in inertial motion)?

ghwellsjr: if yes, what do you mean by the rod's length contraction being merely a coordinate effect, or as WannabeNewton states a "coordinate artifact"? If the rod is contracted and fits in the barn in the barn's frame, isn't its length contractedness in the barn frame a "real effect," using WBN's phrase?

 

[dEdt]

dEdt and ghwellsjr, do you each agree that the pole is entirely within the barn in the barn frame for at least a short period of barn time?

Yes, absolutely.

if yes, does this occur only if the rod is in absolute motion (such that its molecules are contracted due to the behavior of the forces holding the rod together), or do you conclude that there is a behavior of forces on the rod regardless of whether the rod had been accelerated, the barn had been accelerated, or even if one does not know which one was accelerated (given that we are told that there is no absolute motion in inertial motion)?

I'm not 100% sure I understand your question, but I'll answer as best as I can.

Let's say we're in the barn frame and happen to see a rod flying past us. We don't know how the rod reached that speed -- maybe it was traveling that way for its entire existence, maybe it was recently accelerated to that speed, maybe it was traveling even faster in the past and recently decelerated -- nor do we care. Further suppose we have the divine knowledge that the same rod would have a length $L$ along the direction of motion if it were stationary. Then, necessarily, the length of the rod will be $L\sqrt{1-\beta^2}$ in the barn frame.

 

[ghwellsjr]

At the risk of bringing blows down upon myself, can I ask some questions to clarify the two views?

No one gets blows for asking questions here.

Consider the basic barn and pole paradox, where the barn has a front door and a solid rear wall. A pole has greater proper length than the proper length of the barn; the pole and barn are in inertial motion with respect to each other; in the barn frame, the pole is length contracted and enters the barn through the front door; the door closes, and the pole is entirely within the barn (at least for a very short period of time in the barn frame).

That's not the basic barn and pole paradox because it doesn't have a back door which opens at just the right time to let the pole out unharmed. Nevertheless, we can deal with either type of situation.

dEdt and ghwellsjr, do you each agree that the pole is entirely within the barn in the barn frame for at least a short period of barn time?

Yes.

dEdt: if yes, does this occur only if the rod is in absolute motion (such that its molecules are contracted due to the behavior of the forces holding the rod together), or do you conclude that there is a behavior of forces on the rod regardless of whether the rod had been accelerated, the barn had been accelerated, or even if one does not know which one was accelerated (given that we are told that there is no absolute motion in inertial motion)?

ghwellsjr: if yes, what do you mean by the rod's length contraction being merely a coordinate effect, or as WannabeNewton states a "coordinate artifact"? If the rod is contracted and fits in the barn in the barn's frame, isn't its length contractedness in the barn frame a "real effect," using WBN's phrase?

No, it's based on the convention of simultaneity. Conventions are man-made concepts. What's real is the fact that the pole will smash into the rear of the barn and explode it unless something is done to stop it. If you do stop it, the other issue of "contractedness" comes into play.

I have thoroughly analyzed and presented both flavors of this paradox in these two threads. Please study them and see if they answer your questions.

https://www.physicsforums.com/showthread.php?p=4409852

Make sure you read my two posts on the first page of the above thread.

https://www.physicsforums.com/showthread.php?p=4544441

 

[JVNY]

. . . Let's say we're in the barn frame and happen to see a rod flying past us. We don't know how the rod reached that speed -- maybe it was traveling that way for its entire existence, maybe it was recently accelerated to that speed, maybe it was traveling even faster in the past and recently decelerated -- nor do we care. Further suppose we have the divine knowledge that the same rod would have a length $L$ along the direction of motion if it were stationary. Then, necessarily, the length of the rod will be $L\sqrt{1-\beta^2}$ in the barn frame.

This answer assumes that it is the rod that was accelerated and is moving, which is consistent with your earlier posts, which depend upon physical effects from the object moving:

It's a fact that the intermolecular forces in a moving object are different than in a stationary object. Fitzgerald used this observation to predict length contraction." (post 6), and

If you assume that intermolecular forces are electrical in nature then you can deduce, based on how the electric field of a moving point charge compares to a stationary charge, that the size of molecules as well as the intermolecular distance will shrink by a factor of gamma. . . [T]he contraction of a moving body is ultimately due to the behavior of the forces holding that body together, whether or not it's practically feasible to calculate length contraction by analyzing these forces. (post 15)​

But what if the barn had been accelerated? That may seem impractical, so consider a bay in a spaceship. The spaceship could have been accelerated, and a rod floating in outer space would still present length contracted and still fit within the bay as the bay door closes. No forces acted on the rod; all acted on the spaceship.

Perhaps we are speaking past each other. When I say "the pole is entirely within the barn in the barn's frame" I mean that the pole is in the barn before any collision with the barn's rear wall, or before any clamping of the pole (as discussed in the posts that ghwellsjr linked). Just for the brief time after the door closes and before the pole crashes into the back wall, the pole (in its entirety) is inside the barn (is entirely enclosed by the barn) in the barn frame. This occurs because the length of the pole is shorter in the barn frame than in the pole's frame. The pole is already length contracted before any crashing or clamping.

Yet this can occur without any acceleration of the pole, and thus without any forces acting on the molecules of the pole. So I do not understand how the length contraction can be said to occur because of forces on the pole's molecules.

 

[JVNY]

No, it's based on the convention of simultaneity. Conventions are man-made concepts. What's real is the fact that the pole will smash into the rear of the barn and explode it unless something is done to stop it. If you do stop it, the other issue of "contractedness" comes into play.

I have thoroughly analyzed and presented both flavors of this paradox in these two threads. Please study them and see if they answer your questions.

https://www.physicsforums.com/showthread.php?p=4409852

Make sure you read my two posts on the first page of the above thread.

https://www.physicsforums.com/showthread.php?p=4544441

Let's look at the version in which the pole does not burst through the rear wall. I agree generally with your linked diagrams, but I think that there is still a definitional issue about what is "coordinate" versus "real."

Say that the pole is balsa wood, and it enters a cave in an extremely dense mountain, and a door at the mouth of the cave closes. Where your explanation confuses me is in this part of your post 2 in the first link:

if you actually stop the ladder by simultaneously (in the garage frame) forcing each portion of the ladder to stop and stay stopped, then it will end up being shortened. Of course, as they point out later in the article, there's no such thing as a truly rigid ladder and so we have to imagine that this ladder can deform by whatever mechanism caused it to stop.​

As I understand SR, the rod/pole/ladder is already length contracted in the barn/cave when the door closes. The rod is entirely contained in the barn, which can only occur because its length in the barn frame is shorter than the length of the barn (in the barn frame). Clamping the rod does not cause it to "end up being shortened" in the barn frame. It is already length contracted in the barn frame.

Stopping the rod as described only causes the rod to end up shortened in its own frame after it finishes deforming. Even without clamps, the balsa wood pole might simply crash into and be compressed against the rear wall of the cave; or it might crash, compress, then partially expand back toward the door. But it could stay entirely within the cave, although obviously deformed as you mention. And in the cave frame, the pole is within the cave both immediately before it crashes and after it crashes.

Clearly this is not the case in the pole frame. But that is irrelevant. The relativity of simultaneity allows for both of the frames to be equally valid, so it is just as valid for a cave dweller to conclude that the balsa wood pole is "really" entirely within the cave before the crash as it is for a pole rider to conclude that it "really" is not. It seems to devalue the cave frame to say that the length of the pole in the cave frame is not real.

 

[dEdt]

But what if the barn had been accelerated?

In the barn's reference frame, the rod accelerates. As it accelerates the intermolecular forces change, causing it to shrink.

Edit: I'll try to anticipate your next question.

Suppose that we had a spaceship floating in space (where else?) measuring the distance between two stars 4 light-years apart. The spaceship then applies its thrusters, causing the interstellar distance to decrease. From the spaceship's perspective, what's responsible for the change in distance? Surely not "changes in interstellar forces", right?

This example illustrates the difficulties with analyzing things in non-inertial coordinate systems (at least in special relativity). Just as in classical physics, a relativistic non-inertial observer can understand some but not all of the phenomena he witnesses because the laws of physics are simply not the same in his reference frame. From the spaceship's perspective, the observed reduction in interstellar distance can only be explained by analyzing the situation from an inertial reference frame.

But as soon as the spaceship ceases to accelerate, astronauts on board have no difficulty explaining why the distance between the two stars is only 1 light-year -- that's the actual distance, in their reference frame! The only thing that requires explanation is why Earth-based astronauts would disagree and instead conclude that the distance is 4 light-years, and that can be explained by the distortions in their telescopes and other measuring apparatuses due to their motion.

 

[ghwellsjr]

No, it's based on the convention of simultaneity. Conventions are man-made concepts. What's real is the fact that the pole will smash into the rear of the barn and explode it unless something is done to stop it. If you do stop it, the other issue of "contractedness" comes into play.

I have thoroughly analyzed and presented both flavors of this paradox in these two threads. Please study them and see if they answer your questions.

https://www.physicsforums.com/showthread.php?p=4409852

Make sure you read my two posts on the first page of the above thread.

https://www.physicsforums.com/showthread.php?p=4544441

Let's look at the version in which the pole does not burst through the rear wall. I agree generally with your linked diagrams, but I think that there is still a definitional issue about what is "coordinate" versus "real."

Say that the pole is balsa wood, and it enters a cave in an extremely dense mountain, and a door at the mouth of the cave closes. Where your explanation confuses me is in this part of your post 2 in the first link:

if you actually stop the ladder by simultaneously (in the garage frame) forcing each portion of the ladder to stop and stay stopped, then it will end up being shortened. Of course, as they point out later in the article, there's no such thing as a truly rigid ladder and so we have to imagine that this ladder can deform by whatever mechanism caused it to stop.​

As I understand SR, the rod/pole/ladder is already length contracted in the barn/cave when the door closes. The rod is entirely contained in the barn, which can only occur because its length in the barn frame is shorter than the length of the barn (in the barn frame). Clamping the rod does not cause it to "end up being shortened" in the barn frame. It is already length contracted in the barn frame.

Stopping the rod as described only causes the rod to end up shortened in its own frame after it finishes deforming. Even without clamps, the balsa wood pole might simply crash into and be compressed against the rear wall of the cave; or it might crash, compress, then partially expand back toward the door. But it could stay entirely within the cave, although obviously deformed as you mention. And in the cave frame, the pole is within the cave both immediately before it crashes and after it crashes.

Clearly this is not the case in the pole frame. But that is irrelevant. The relativity of simultaneity allows for both of the frames to be equally valid, so it is just as valid for a cave dweller to conclude that the balsa wood pole is "really" entirely within the cave before the crash as it is for a pole rider to conclude that it "really" is not. It seems to devalue the cave frame to say that the length of the pole in the cave frame is not real.

I like the way you continually state "in the barn/cave frame" when discussing issues of time and length. That's very important. But we cannot simply say the rod/pole/ladder frame because it is at rest in two different inertial frames. We can use that terminology for the normal version of the paradox where the object remains inertial, but in this version we have to say something like the rest frame of the pole/rod/ladder prior to its being clamped to a stop.

Besides that issue, right at the end, you equate a frame with an observer when you refer to the "cave dweller" or the "pole rider" as if what the cave frame depicts is what's real for the cave dweller or what the pole frame depicts is what's real for the pole rider. This was my fifth objection in post #5 of the linked thread that you are talking about:

5) In their explanation for Figure 8 they repeatedly use the words "sees", "see" and "seen" and apply it to a person, which is incorrect. No person anywhere in any scenario can see what is depicted in a spacetime diagram unless light signals are also drawn in. They did not draw them in any of their diagrams. If you do drawn them in, it won't matter which frame you use, they all will show the same thing for what any observer sees.

What the pole or ladder rider sees is what's real. What the cave or barn dweller sees is what's real. If we were to go to the effort of drawing in 45-degree lines from various events to the locations of these observers, we would see that it doesn't matter what frame we do it in. They cannot tell just by observations what the frames depict. That means that they cannot observe length contraction and the only way they can determine the length contraction that a particular frame depicts is if they actually send out and receive radar signals and assume that the signals take the same amount of time going as coming to determine a distance and assign that distance to the average of the sent and received time, then they can make a diagram of their individual rest frame. For an inertial observer like the barn dweller, he will end up with the same diagram as the one I already drew for the rest frame of the barn and he can transform to any other inertial frame. But for the ladder rider, depending on where he is on the ladder, he will get a different diagram than any portion of either of the two diagrams that I drew. This is because he is non-inertial and his rest frame is going to be non-inertial. But he can then use that information and the knowledge that the barn is inertial to construct the same diagram that the barn dweller made and from there he can transform to any other inertial frame. The barn dweller can also derive the non-inertial frame of the ladder rider.

So none of these diagrams depicts anything more real than any other and since length contraction is different in each one, it cannot be said to be real. But all the diagrams depict what is actually real for any observer, namely, what they can actually see and measure.

 

[Sugdub]

...But remember, length (or distance) contraction is merely a coordinate effect. When we change reference frames and use the Lorentz Transformation process, the time and length (or distance) coordinates change. Nothing has actually changed to the objects or the space. The same can be said for Time Dilation.

Indeed I like this. Do you agree that “we” does not stand for “the observer” (I mean anybody involved in the experiment and who receives physical signals) but “we physicists who formalize the physical scenario” (I mean a theoretician who is not necessarily involved in the experiment)? Just remember the “moving magnet and conductor” experiment described by Einstein: nowhere he needs to specify where the “observer” stands, it's enough to know that the device which measures the intensity of the current (the physical quantity which gets “observed”) is tied to the conductor.

The former Newtonian mechanics did not enforce such a change in the formal description of the world. It did not impose that physical quantities such as the spatial length and the time duration separating two physical events be assigned different numerical values, via the Lorentz transformation, depending on the IRF selected by the theoretician to represent the coordinates of those events. Hence it did not impose homogeneous descriptions of the world whereby the relevant physical quantities must be defined in respect to the same IRF. For example the thickness of the atmosphere is usually defined in the rest frame of the Earth, whereas the lifetime of a muon is defined in its own rest frame. On that basis the former Newtonian mechanics could not explain that a fast-enough muon can reach the ground before decaying. Only the SR theory, because it imposes to relate the numerical value of physical quantities to the same IRF, whichever one is selected, is able to predict that outcome, irrespective of the selected IRF: a fast-enough muon can reach the ground. Please note that no reference is made to any kind of “observer”.

IMHO the "barn and ladder" scenario should be discussed in the same way: should their respective length be related to the same IRF, whichever is selected, a fast-enough ladder would entirely fit in the barn. Is this correct?

Observers in a scenario cannot tell that we switched to a different reference frame when we did the above exercise and so nothing changes either in what they see, what they measure, or what they observe. In fact, Length Contraction and Time Dilation are completely unobserverable. They can only be determined by observers by proactively sending out radar signals, waiting for their echoes, observing clocks on other objects, logging all the data and the times they occurred according to their own clock and then doing a lot of computation. Only after the entire scenario is over will they be able to go back and make diagrams like I did and see those coordinate effects.

Do you agree that “we” refers to the theoretician who analyze a unique scenario through different formal representations (different IRFs), whereas “they” stands for the “observer(s)” who is (are) involved in this unique scenario through performing measurements or observations (and who therefore must receive enabling signals)?
Nothing changes in the observable world due to the decision by the theoretician to describe the same scenario alongside a different framework. Changing IRF does not trigger any physical effect, and this is why no change can be “observed”. Your diagrams perfectly illustrate that the propagation of signals toward the “observer” overlays the SR-induced description of the world with 45° lines representing light rays and entails a Doppler effect which affects the outcome of “observations” through a genuine physical (Doppler) effect. Unfortunately most debates about SR fail to clearly distinguish both layers and misuse the words “see”, “observe” or “measure”.

 

[JVNY]

dEdt and ghwellsjr, thanks. These are certainly very different approaches; it will be interesting to think more about whether they are distinct, or rather different components relativized to a given observer as WannabeNewton suggests.

 

[dEdt]

dEdt and ghwellsjr, thanks. These are certainly very different approaches; it will be interesting to think more about whether they are distinct, or rather different components relativized to a given observer as WannabeNewton suggests.

The two approaches are closely related, and I'll outline how but first I need to make an important point.

Again consider a rod moving in an inertial reference frame. Some people in this thread seem to deny that it is possible to use the laws of physics (as expressed in this reference frame) to deduce that the rod will contract without performing any coordinate transformations. These people are simply wrong. To see why, consider a simpler system: a hydrogen atom in its ground state. If this atom is at rest, it is a simple undergrad-level application of quantum mechanics to calculate the size of the electron orbital. If the atom is moving, while the calculation would become much more involved it is still possible in principle to deduce the new size of its electron orbital. Anyone who argues otherwise is, in effect, arguing that the laws of physics don't apply to objects in motion. And as we all know, we would find that the electron orbital is compressed along the direction of motion compared to the electron orbital at rest. What's true for a hydrogen atom is true for a measuring rod or any other system imaginable.

So, what's the relationship between the physical contraction of a moving rod and coordinate transformations?

While it's possible to calculate the size of a moving rod in the reference frame where it is moving, such an endeavor would obviously be foolish because it would involve probably the most difficult calculation in condensed matter physics ever undertaken. Thankfully there's a simpler way: we exploit the Principle of Relativity.

The Principle of Relativity asserts that there exists a new coordinate system where 1) the rod is at rest, and 2) the laws of physics are the same. This is fantastic because in this new coordinate system we don't need to calculate the length of the rod! We already know it has to be $L$, the rest length of the rod in the original reference frame, because the laws of physics are the same. So in order to find the length of the rod in the original frame, we just apply a coordinate transformation back to the original coordinate system. And thankfully Einstein already deduced what coordinate transformations preserve the laws of physics: these are just the Lorentz transformations. So by applying a Lorentz transformation back to the original coordinate system, we find that the length of the rod is $L\sqrt{1-\beta^2}$.

This second approach does not deny that the rod contracts because of the behavior of its intermolecular forces. Rather, it sidesteps having to work out the details of how these forces change when the rod moves by exploiting the fact the laws governing the intermolecular forces (quantum electrodynamics) are invariant under a Lorentz transformation.

 

[ghwellsjr]

Indeed I like this. Do you agree that “we” does not stand for “the observer” (I mean anybody involved in the experiment and who receives physical signals) but “we physicists who formalize the physical scenario” (I mean a theoretician who is not necessarily involved in the experiment)? Just remember the “moving magnet and conductor” experiment described by Einstein: nowhere he needs to specify where the “observer” stands, it's enough to know that the device which measures the intensity of the current (the physical quantity which gets “observed”) is tied to the conductor.

Yes, when I said "we", I meant all of us that are defining, describing, analyzing, and discussing a thought experiment. We imagine observers experiencing the thought experiment.

The former Newtonian mechanics did not enforce such a change in the formal description of the world. It did not impose that physical quantities such as the spatial length and the time duration separating two physical events be assigned different numerical values, via the Lorentz transformation, depending on the IRF selected by the theoretician to represent the coordinates of those events. Hence it did not impose homogeneous descriptions of the world whereby the relevant physical quantities must be defined in respect to the same IRF. For example the thickness of the atmosphere is usually defined in the rest frame of the Earth, whereas the lifetime of a muon is defined in its own rest frame. On that basis the former Newtonian mechanics could not explain that a fast-enough muon can reach the ground before decaying. Only the SR theory, because it imposes to relate the numerical value of physical quantities to the same IRF, whichever one is selected, is able to predict that outcome, irrespective of the selected IRF: a fast-enough muon can reach the ground. Please note that no reference is made to any kind of “observer”.

IMHO the "barn and ladder" scenario should be discussed in the same way: should their respective length be related to the same IRF, whichever is selected, a fast-enough ladder would entirely fit in the barn. Is this correct?

In the barn frame, yes. I hope the two threads I pointed to in post #20 made that very clear.

Do you agree that “we” refers to the theoretician who analyze a unique scenario through different formal representations (different IRFs), whereas “they” stands for the “observer(s)” who is (are) involved in this unique scenario through performing measurements or observations (and who therefore must receive enabling signals)?

Yes, but I also pointed out that any observer can also be a theoretician, assuming that we let them perform the relevant experiments.

Nothing changes in the observable world due to the decision by the theoretician to describe the same scenario alongside a different framework. Changing IRF does not trigger any physical effect, and this is why no change can be “observed”. Your diagrams perfectly illustrate that the propagation of signals toward the “observer” overlays the SR-induced description of the world with 45° lines representing light rays and entails a Doppler effect which affects the outcome of “observations” through a genuine physical (Doppler) effect. Unfortunately most debates about SR fail to clearly distinguish both layers and misuse the words “see”, “observe” or “measure”.

How true.

 

[Bill_K]

And as we all know, we would find that the electron orbital is compressed along the direction of motion compared to the electron orbital at rest. What's true for a hydrogen atom is true for a measuring rod or any other system imaginable.

This is what Lorentz was forced to assume, and why his viewpoint lost out to Einstein's. All Lorentz really had to go on was the fact that a moving Coulomb field appears contracted. But the world is made of other things besides electromagnetism. The shape of planetary orbits for example is determined by Newtonian gravity. How does Newtonian gravity transform under a velocity boost? We now know that gravity does NOT transform the same way as electromagnetism.

And the shape of nuclei (or neutron stars) must change exactly the same way too. But even without knowing of the existence or nature of the nuclear force, Lorentz had to hypothesize that all forces underwent an identical contraction. Einstein of course replaced this ad hoc assumption with the much simpler idea that space itself was responsible.

What clinched the argument in Einstein's favor was the realization that relativity applied to particle kinematics as well, which Lorentz's theory did not.

 

[Mentz114]

This second approach does not deny that the rod contracts because of the behavior of its intermolecular forces. Rather, it sidesteps having to work out the details of how these forces change when the rod moves by exploiting the fact the laws governing the intermolecular forces (quantum electrodynamics) are invariant under a Lorentz transformation.

Suppose we have three mobile laboratories and in one there is an instrument with a digital readout measuring a rod. The other two labs speed off and use some method to measure the rod (in the first lab) themselves . They find that their measurements give a smaller number than the digital readout which they can also see.

All measurements are made when the 3 labs are moving inertially. Did the rod experience any strain or change in molecular configuration because the other two labs made a measurement ?

If the two labs made their remote measurements so that they were simultaneous in the rod frame, how did the rod sustain two different states at the same time ?

 

[dEdt]

This is what Lorentz was forced to assume, and why his viewpoint lost out to Einstein's. All Lorentz really had to go on was the fact that a moving Coulomb field appears contracted. But the world is made of other things besides electromagnetism. The shape of planetary orbits for example is determined by Newtonian gravity. How does Newtonian gravity transform under a velocity boost? We now know that gravity does NOT transform the same way as electromagnetism.

And the shape of nuclei (or neutron stars) must change exactly the same way too. But even without knowing of the existence or nature of the nuclear force, Lorentz had to hypothesize that all forces underwent an identical contraction. Einstein of course replaced this ad hoc assumption with the much simpler idea that space itself was responsible.

What clinched the argument in Einstein's favor was the realization that relativity applied to particle kinematics as well, which Lorentz's theory did not.

Yes, you're absolutely correct. Einstein's approach allowed people to calculate things like the length contraction of an atomic nucleus without having to know all the laws of physics, if the laws of physics are assumed to be Lorentz invariant. However, this doesn't mean that Lorentz was wrong to state the Lorentz contraction could in principle be explained by looking at the forces holding something together. As Pauli put it,

Should one, then, completely abandon any attempt to explain the Lorentz contraction
atomistically? We think that the answer to this question should be No. The contraction
of a measuring rod is not an elementary but a very complicated process. It would not take
place except for the covariance with respect to the Lorentz group of the basic equations
of electron theory, as well as of those laws, as yet unknown to us, which determine the
cohesion of the electron itself.

 

[dEdt]

All measurements are made when the 3 labs are moving inertially. Did the rod experience any strain or change in molecular configuration because the other two labs made a measurement ?

The molecular configuration of the rod did change (namely, the molecules compressed and got closer to each other), but not as a result of the measurement. It came about because of the rod's motion.

If you keep in mind that force is not a Lorentz invariant quantity, you'll see that there's no contradiction in having three observers reach different conclusions about the nature of the intermolecular forces acting in a rod.

 

[Mentz114]

Thank you for trying to explain my doubts. But ...

...
It came about because of the rod's motion.
..

But the motion is relative, so the rod must have a nearly infinite number of configurations simultaneously.

If you keep in mind that force is not a Lorentz invariant quantity, you'll see that there's no contradiction in having three observers reach different conclusions about the nature of the intermolecular forces acting in a rod.

But the motion is inertial so there are no forces involved. How does the motion change the molecular configuration ?

 

[dEdt]

But the motion is relative, so the rod must have a nearly infinite number of configurations simultaneously.

I think it's more accurate to say there there are an infinite number of different ways to describe the configuration of the rod, one for each reference frame.

Let's step away from something as complicated as a rod and look at something simpler, like a point charge. Figure 1 shows the electric field produced by a stationary point charge.

http://upload.wikimedia.org/wikipedia/commons/b/b9/Relativistic_electromagnetism_fig3.svg

Figure 2 shows the electric field produced by a moving charge.

http://upload.wikimedia.org/wikipedia/commons/b/b2/Relativistic_electromagnetism_fig4.svg

Clearly there's a difference between the two electric fields -- a difference that arises from the point charge's motion.

An observer at rest relative to the point charge will always see Figure 1, while an observer moving relative to the will always see Figure 2. Is it correct to say that there are two (or more) different configurations of the electric field? I don't think so. Better to say that there are two different descriptions of the electric field.

But the motion is inertial so there are no forces involved. How does the motion change the molecular configuration ?

There are no external forces on the rod, but there are plenty of internal forces.

 

[Mentz114]

I think it's more accurate to say there there are an infinite number of different ways to describe the configuration of the rod, one for each reference frame

(my emphasis)

Sure, from a moving POV the charge distribution/rod looks different. But nothing happened to the rod, because there's no physical difference between inertial motion and rest.

None of these arguments demonstrate more than the fact that things are different when measured (described ?) from a moving POV. Which we expect. But the rod is unchanged by this.

There are no external forces on the rod, but there are plenty of internal forces.

Which remain unchanged for the rod in any state of inertial motion.

 

[bahamagreen]

My old book says...

The Hamiltonian for the atom will have operators that only operate on the coordinates of the particular particles, but it also includes motion of the atom as a whole (the center of mass).

So the Schrodinger equation may be separated, and the eigenfunctions connected only through a common separation constant, which includes the kinetic energy of the center of mass of the atom.

So unless the atom is "in a box", the KE can assume any value, so the eigenfunctions are independent* of each other, and the internal state of the atom is independent of the motion of its center of mass.

*In the event that the separation constant, itself, is quantized; the factors of the eigenfunctions may be only conditionally independent.

 

[dEdt]

But nothing happened to the rod, because there's no physical difference between inertial motion and rest.

Not true. The laws of physics in any given reference frame make a clear distinction between objects at rest and objects in motion. Just take a look at the difference between a stationary point charge and a moving point charge. Don't confuse the this fact with the claim that the laws of physics are the same for observers moving with constant velocity relative to each other.

None of these arguments demonstrate more than the fact that things are different when measured (described ?) from a moving POV. Which we expect. But the rod is unchanged by this.

If the rod were unchanged by motion, it wouldn't shrink.

Which remain unchanged for the rod in any state of inertial motion.

Again, not true. Forces are not Lorentz covariant.

 

[dEdt]

My old book says...

The Hamiltonian for the atom will have operators that only operate on the coordinates of the particular particles, but it also includes motion of the atom as a whole (the center of mass).

So the Schrodinger equation may be separated, and the eigenfunctions connected only through a common separation constant, which includes the kinetic energy of the center of mass of the atom.

So unless the atom is "in a box", the KE can assume any value, so the eigenfunctions are independent* of each other, and the internal state of the atom is independent of the motion of its center of mass.

*In the event that the separation constant, itself, is quantized; the factors of the eigenfunctions may be only conditionally independent.

It sounds like you're using non-relativistic quantum mechanics. If you use QED, you'll see that your claim isn't true.

 

[Mentz114]

If the rod were unchanged by motion, it wouldn't shrink.

I'm asserting that the rod does not shrink. How can my motion affect some independent object ? Therefore I see no need to invoke any additional physics to 'explain' the relativistic effect, viz that measuring something in motion will give smaller number than the rest frame measurement.

But nothing happened to the rod, because there's no physical difference between inertial motion and rest.

Again, not true. Forces are not Lorentz covariant.

You misunderstand me because you are assuming the rod shrinks and trying to explain 'how' using an irrelevant and speculative mechanism.

 

[dEdt]

I'm asserting that the rod does not shrink. How can my motion affect some independent object ?

Well, your assertion is simply incorrect. That a moving object shrinks can be deduced from the Lorentz invariance of the laws of physics, and the Lorentz invariance of the laws of physics is an experimental fact built into all fundamental theories of physics since the 20th century. To deny the reality of Lorentz contraction is either to deny modern physics or to use a non-standard definition of the length of an object.

Presumably you also don't believe in time dilation ie that processes take longer when in motion than
when at rest. How exactly do you explain the experimental verifications of time dilation?

If you want to understand how motion "[can] affect some independent object", just look at Maxwell's equations. The equations contain a current density term, which depends on the motion of the charge distribution. Hence then laws of physics -- at least as expressed in a particular inertial coordinate system -- affect objects in different ways depending on their motion. If that seems unintuitive to you, then your intuition is simply wrong.

 

[Mentz114]

Well, your assertion is simply incorrect. That a moving object shrinks can be deduced from the Lorentz invariance of the laws of physics, and the Lorentz invariance of the laws of physics is an experimental fact built into all fundamental theories of physics since the 20th century. To deny the reality of Lorentz contraction is either to deny modern physics or to use a non-standard definition of the length of an object.

Obviously, I disagree. And for the record I define the length of an object as the result of the measurement in the objects rest frame.

Presumably you also don't believe in time dilation ie that processes take longer when in motion than when at rest. How exactly do you explain the experimental verifications of time dilation?

Time dilation has never been directly experimentally verified which gives it the same ontological status as length contraction. What has been verified is that the elapsed time on a clock is the proper interval of its worldline between events.

If you want to understand how motion "[can] affect some independent object", just look at Maxwell's equations. The equations contain a current density term, which depends on the motion of the charge distribution. Hence then laws of physics -- at least as expressed in a particular inertial coordinate system -- affect objects in different ways depending on their motion. If that seems unintuitive to you, then your intuition is simply wrong.

I think this is irrelevant. Also, I don't rely on intuition.

I'll make two more points

1. the outcome of the barn-pole paradox ( viz, that the pole which is slightly longer then the barn when they are measured at rest) is as if both the pole and barn did not shrink or expand. So no direct evidence for length contraction ( but lots for relativity of simultaneity ).

2. If the distance ( space ) between two objects at rest wrt each other is measured from a moving platform, it will give a result smaller than the rest frame measurement. What made the empty space shrink ?

I'm tired so I won't be able to reply ( should you persist ) until tomorrow on my clock.

 

[stevendaryl]

Obviously, I disagree. And for the record I define the length of an object as the result of the measurement in the objects rest frame.

Some of the disagreement here may simply be a clash of definitions. If you define length in a frame to be the distance between two ends measured simultaneously, then a rod does shrink when you accelerate it from rest. If you define it your way, it doesn't shrink.

 

[dEdt]

And for the record I define the length of an object as the result of the measurement in the objects rest frame.

Well then it's practically a tautology to say that the length of an object isn't affected by motion. However, if you define length as the distance between the endpoints of an object measured simultaneously -- which is how almost everyone defines it -- then you are forced to the conclusion that objects compress under motion.

Time dilation has never been directly experimentally verified

No. Muons in cosmic rays decay more slowly than muons at rest in the laboratory.

2. If the distance ( space ) between two objects at rest wrt each other is measured from a moving platform, it will give a result smaller than the rest frame measurement. What made the empty space shrink ?

The question is not, what made the empty space shrink, but rather, why do the two observers disagree about the distance between the two objects. To the observer on the moving platform, the reason an observer at rest wrt the object measures a greater distance is because he is using measuring rods which are contracted.

 

[Mentz114]

Well then it's practically a tautology to say that the length of an object isn't affected by motion. However, if you define length as the distance between the endpoints of an object measured simultaneously -- which is how almost everyone defines it -- then you are forced to the conclusion that objects compress under motion.

No, your point below allows me to say that there is no compression - only that my rulers are different.

I think this contradicts what you say here

The question is not, what made the empty space shrink, but rather, why do the two observers disagree about the distance between the two objects. To the observer on the moving platform, the reason an observer at rest wrt the object measures a greater distance is because he is using measuring rods which are contracted.

Again I assert that length contraction is a relativistic effect which makes any measurement on a moving object give a smaller number that the rest-frame measurement. It does not imply that the object is compressed, only that different 'rulers' ( coordinates) are being used. The Lorentz transformation gives the relationship between the clocks and rulers in the two frames, it does not imply that the object has changed.

You have to choose between 'object compresses' or 'rulers are different'. You don't need both and the second requires no additional physics.

 

[Mentz114]

Some of the disagreement here may simply be a clash of definitions. If you define length in a frame to be the distance between two ends measured simultaneously, then a rod does shrink when you accelerate it from rest. If you define it your way, it doesn't shrink.

Sure. But a property of an object has the value that the object itself assigns. Suppose you measured yourself to be x meters from head to toe. I make a remote moving measure and tell you that you are actually y meters from head to toe. Who are you going to believe ?
Put the 'proper' back in 'property'.

 

[stevendaryl]

Sure. But a property of an object has the value that the object itself assigns.

Who says? I don't think that's a consistent approach. For instance, light certainly has properties--frequency, wavelength, momentum--but it doesn't make sense to ask what properties the light assigns itself, because there is no such thing as the rest frame of light.

 

[Mentz114]

Who says? I don't think that's a consistent approach. For instance, light certainly has properties--frequency, wavelength, momentum--but it doesn't make sense to ask what properties the light assigns itself, because there is no such thing as the rest frame of light.

I don't think this is relevant because light is not an object. Length contraction is a kinematic effect between timelike worldlines.

If it is merely a convention how one defines length, then I choose the rest frame measurement. The point I'm trying to make is that there's nothing in SR that requires 'the rod' to become compressed. There is only one rod, yes ?

 

[FactChecker]

Hi. I know that space for an object in motion will contract, relative to an observer. We generally read that space contracts for the object in the direction of motion. But doesn't space around the object also contract? Can someone clarify this? Thanks.

"around the object" -- If you are asking about distances measured perpendicular to the direction of motion, then no. Those measurements do not change. Both reference frames agree about distances in those directions.

If you are asking about measuring the rocket compared to the space that it is in, then yes. Everything apparently shrinks in that direction. So the moving person cannot detect any change in his own rocket size. The change in length is only apparent to the people in the "stationary" reference frame. Suppose I am stationary and you are in the rocket. Before you start moving, we have identical length rulers and agree that your rocket is 100 ft long. When you are traveling, you still measure your rocket as 100 ft long using your (shrunken) ruler. I think that your rocket is shorter. I understand why you still think it is 100 ft because your ruler has shrunk the exact same amount. So your ruler is wrong and your 100 ft measurement has become wrong.

 

[stevendaryl]

I don't think this is relevant because light is not an object.

That reinforces my point--that it isn't a consistent approach to talk about properties with respect to objects. If you take an extended object, such as a train, and start accelerating it, there IS no such thing as "the rest frame of the object" because in general, different parts of the object are traveling at different speeds.

If you pick an inertial Cartesian coordinate system to describe motion and distance and so forth, then it will be the case that:

1. Take a "rigid" rod that initially has length L when at rest. Gently accelerate it in the direction of its length to a new speed v. Allow it to come to an equilibrium length at the new speed. Then that length will be L \sqrt{1-\frac{v^2}{c^2}}.
2. Take a metronome, or windup clock, or something that regularly emits a "tick" at an interval of time T when at rest. Gently accelerate it to a new speed v. Afterward, it will tick with an interval given by \dfrac{T}{\sqrt{1-\frac{v^2}{c^2}}}

These are facts. Now, it is the case that Minkowsky spacetime allows these facts to be given a "geometric" interpretation: There is an intrinsic length for rods and an intrinsic tick rate for metronomes, and the measured length and rate is computed by a kind of geometric projection. But the fact that it has a geometric explanation doesn't negate the length contraction and time dilation, it just explains it.

 

[WannabeNewton]

But the fact that it has a geometric explanation doesn't negate the length contraction and time dilation, it just explains it.

I agree wholeheartedly with the rest of your post but I'm going to have to just slightly disagree here. Length contraction isn't explained in SR in the constructive sense if you use the relativity of simultaneity (i.e. a relativized chronogeometric structure of space-time) as the basis of the derivation whereas it is explained in Lorentz ether theory in terms of the microscopic Maxwell equations in the constructive sense. In other words the former falls out of chronogeometric assumptions of SR whereas the latter is a consequence of dynamics.

That being said, dEdt you should stop arguing your position as if it's a black and white issue in your favor because it isn't. While length contraction being explained dynamically by the microscopic Maxwell equations is an uncontentious part of Lorentz ether theory, the same doesn't go for SR. There is a profuse of literature in the philosophy of physics still debating whether the same constructive dynamical explanation of length contraction can be extended to the framework of SR in place of Einstein's non-constructive chronogeometric derivation of length contraction. You should probably read up on the literature first before trying to act as if you're 100% in the right.