Whats the best way to describe this system?

[megr_ftw]

I have done problems similar to this one with 4 components but I am getting stumped with this one.
The probability of failure for each components is next to the number

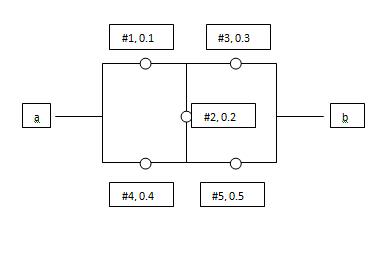
i basically need to find the probability that the system works..but the 5th component is confusing me
so far I have system fails= (A1UA4)UA2U(A3UA5), then you can just subtract 1 to get success

im wondering how to set up prob of success using intersections and unions.. and a method to find this so i don't have to post everytime i have a question :p

 

[CRGreathouse]

so far I have system fails= (A1UA4)UA2U(A3UA5), then you can just subtract 1 to get success

I get 1(3 + 25) + 4(5 + 23), using + for "or" and concatenation for "and". Your answer, (1 + 4) + 2 + (3 + 5) -- was that trying to be 14 + 2 + 35? -- disagrees with mine.

 

[megr_ftw]

well i think there is also another way to do this problem.
B can represent the entire system.
P(B)= P(A2)*P(B|A2)+P(A2')*P(B|A2') where | means given and ' means not

so if that's true how would i calculate the probabilities?

 

[CRGreathouse]

P(B)= P(A2)*P(B|A2)+P(A2')*P(B|A2') where | means given and ' means not

so if that's true how would i calculate the probabilities?

This statement is true but won't let you compute probabilities.

 

[SW VandeCarr]

It's not clear to me what is required for the system to work. Is it supposed to be redundant? Will any operative path from a to b be sufficient for the system to work? It appears component two not redundant so it looks like two possible directed paths from a to b. Note the probability of system failure is the highest single component probability of failure on a critical path.

 

[megr_ftw]

ways for the system to work are either of the following:
1-3, 4-5, 1-2-5, 4-2-3

 

[SW VandeCarr]

ways for the system to work are either of the following:
1-3, 4-5, 1-2-5, 4-2-3

OK. Then path 1,3 has the lowest maximum single component failure rating with component three having P(F)=.03. If component one fails, that's still within the 3% failure expectation. It doesn't matter if they both fail. So P(S)=0.97.

However, from your original equation, it looks like component 2 is not redundant. That's a more interesting problem. What would P(S) be in that case?

 

[megr_ftw]

well 2 is there if 3 AND 4 fails. 0.97 seems like a likely probablity though...

 

[SW VandeCarr]

well 2 is there if 3 AND 4 fails. 0.97 seems like a likely probablity though...

Yes, if component two can be bypassed. But we just don't give answers here. If you understand the problem, you should be able to compute P(S) if 2 can't be bypassed. It's not hard.

 

[CRGreathouse]

SW VandeCarr, you can't ignore the failure chances for parts other than those most likely to fail. In a simplified model where you need only component A or B to work, failing at rates of 3% and 5%, the overall failure rate is not 5% but 1 - .03 * .05 = 99.85%.

I gave the answer in post #2, except for the calculation which is just addition and multiplication.

 

[SW VandeCarr]

SW VandeCarr, you can't ignore the failure chances for parts other than those most likely to fail. In a simplified model where you need only component A or B to work, failing at rates of 3% and 5%, the overall failure rate is not 5% but 1 - .03 * .05 = 99.85%.

I gave the answer in post #2, except for the calculation which is just addition and multiplication.

The way I would run the system is to run the paths with highest probability of failure (4%, %5%) first until failure. Then the system switches to the path with the 3% failure rate. At any given point in time the expected failure rate is 3% and P(S)=97%. Your way would default to a higher fail rate and the average success rate is k1(1-.03)+k2(1-.05)/2. where ki are time weightings for the lower and higher fail rates. In my model, if we get to the 3% path, higher fail rate paths would be shut off at first failure so the overall fail rate cannot be greater than 3% unless of course this path also fails.

GR I don't see this as a joint probability problem unless you run all paths at once. Then the fail rate is as you say (.03)(.05), but this is not what happens if 3 fails. Then you simply have the line with the 5% fail rate. I'm thinking series rather parallel processing , so perhaps I misunderstood.

 

[megr_ftw]

that makes a lot more sense now. now one hard question I am trying to figure out from that is the probability that component 2 works if the system works. so does this mean you have to go through component 2?

 

[SW VandeCarr]

megr_ftw;2926883]that makes a lot more sense now. now one hard question I am trying to figure out from that is the probability that component 2 works if the system works. so does this mean you have to go through component 2?

The system can work, the way you set up, if 2 fails. Only operative paths then are the 4,5 and the 1-3. I would run the 4,5 until failure with the 1-3 backup. That way you have no more than 3% expected failure. The paths through component 2 have maximum single component fail rates of 4% and 5%, so it's nice to have, but the system can function without them. To know if component 2 is working you have to shut down 4,6 and 1,3.

The the probability of success if you force the paths through component 2 would be what?

EDIT: Forget what I said if your running all paths at once. Then you do use joint probabilities as long as there are no failures or you're not forcing certain paths over others. So if 1,3 and 4,5 are both open, P(S) is 99.85%. For testing component 2 your joint probability of failure is (.04)(.05) P(S)=99.8%.

 

[megr_ftw]

probability of success is .998 correct?

so if component 2 works if system works the prob. would increase right?

 

[megr_ftw]

.998 then?

 

[SW VandeCarr]

.998 then?

There are combinations of component failures that will require component 2 to function. When this happens, system P(S) will drop. I typed an analysis of these but it disappeared. Possibly it was deleted because I was helping you too much. Find the combinations of component failure that force component 2 to function as a necessary component for system function and determine P(S) based on maximum single component failure rating.

 

[megr_ftw]

well to get it straight i got .801 for probability of success...

 

[SW VandeCarr]

well to get it straight i got .801 for probability of success...

How did you get that?

 

[megr_ftw]

i converted everything to prob. of success for each component first
(A1^A3)U(A4^A5)U(A1^A2^A5^A3'^A4')U(A4^A2^A3^A1'^A5') where ^ is intersect and ' is NOT, or failure...
(.9*.7-.63*.3)+(.9*.8*.5*.3*.4)+(.6*.8*.7*.1*.5)=0.801

this is probability a long way to do this but the only way i know how

 

[SW VandeCarr]

i converted everything to prob. of success for each component first
(A1^A3)U(A4^A5)U(A1^A2^A5^A3'^A4')U(A4^A2^A3^A1'^A5') where ^ is intersect and ' is NOT, or failure...
(.9*.7-.63*.3)+(.9*.8*.5*.3*.4)+(.6*.8*.7*.1*.5)=0.801

this is probability a long way to do this but the only way i know how

I think you've missed the whole concept of maximum single component failure rating for a given path. The failure rating for a given path is just the maximum failure rating for a pass-through component on that path.

 

[megr_ftw]

well crap... i know there are only 4 paths it could take so using that notion i did that calculation

 

[SW VandeCarr]

well crap... i know there are only 4 paths it could take so using that notion i did that calculation

Just write out the path component sequences such as 4,2,3.

 

[megr_ftw]

ive been work on this for a while and for the probability that component 2 works given the system works I got 0.76.
and for the probability that component 3 works given the system works I got 0.604...
anyone want to check that because i followed my notes from my teacher and applied them the way i think using conditional probability

 

[bpet]

Hmm, I wonder, if the system was a ladder with 10 rungs (instead of 1), how would the failure probability be calculated?

 

[megr_ftw]

what?

 

[SW VandeCarr]

Did some research. The usual way to determine reliability of components in series is to multiply the individual P(S) so for say for 4,2,3 it's (0.96)(0.98)(0.97)=0.9126.

http://www.reliasoft.com/newsletter/3q2002/availabilities.htm

 

[SW VandeCarr]

The time to failure approach would seem to favor the 'maximum single component failure rating P(F)" as the best way to approach the issue of failure of a path of components in series. However reliability is calculated as the product of 1-P(F) over on the path. Reliability (R) vs time to first failure (TTF) are two models which give different results, so I'm not sure which model is best for this problem. However R seems more common in the literature. Assuming all components are the same age, TTF would seem to be a better measure but may be controversial.

http://media.wiley.com/product_data/excerpt/85/04700948/0470094885.pdf Go to page 5 (sec 1.2.1)

In a related issue of conditional probabilities as to what is the probability that Ai works if the system works requires one to know both P(sAi|sSys) and P(sSys|sAi). Since the probability that the component works P(sAi) and that the system works P(sSys) are not independent, the dependency of these two must be defined by isolating all paths which link a to b and have component Ai .