When does a cantilever beam fail in reality?

[Thomas Plank]

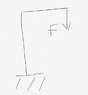
Hi, like the title says, how do we actually calculate when a cantilever beam fails in reality? We’ve been taught that these are absolutely fixed to the ground. However, in reality these would probably be bolted onto the ground, so how do we calculate the force trying to lift the fixed beam on the floor, created by the force at the end of the cantilever if the beam is fixed by something that would fail? I’ve attached a terribly drawn diagram above.

Thank you.

 

[Grinkle]

We’ve been taught that these are absolutely fixed to the ground.

More likely you were given an exercise that modeled the beam as the only flexible element in the problem. What you want to do is to model the beam being attached to a material that also has material properties (aside from being perfectly rigid I mean).

It has been many years since I've solved such problems - but off the top of my head, I think the simplest approach is to define the beam as being perfectly rigid and attached to a material with a modulus and a plastic failure point at some amount of strain. Then you can calculate what forces on the beam cause the mount to fail.

 

[Thomas Plank]

More likely you were given an exercise that modeled the beam as the only flexible element in the problem. What you want to do is to model the beam being attached to a material that also has material properties (aside from being perfectly rigid I mean).

It has been many years since I've solved such problems - but off the top of my head, I think the simplest approach is to define the beam as being perfectly rigid and attached to a material with a modulus and a plastic failure point at some amount of strain. Then you can calculate what forces on the beam cause the mount to fail.

It’s actually been quite a while for me too, I’ve forgot most of what I learned too; how would I actually model as attached to a material with modulus and plastic failure?

All I have right now is the force pushing the beam down and the tensile stress the bolts fail if fixed to concrete. I’m struggling to resolve anything because I can calculate the moment at the mount but that still isn’t enough information to find the lifting force on the mount created by the force at the end of the beam.

 

[Grinkle]

What is the context of the question? Homework vs you are really trying to design something vs pure self-teaching?

My responses would differ based on that.

 

[Thomas Plank]

What is the context of the question? Homework vs you are really trying to design something vs pure self-teaching?

My responses would differ based on that.

This is me trying to design something, I was told by my supervisor at work to just add the mass of the beam on to work it out; unfortunately, I’m not getting anywhere with that hint nor the notes I took at university...

 

[Grinkle]

I see.

I don't know how you can find appropriate bulk material properties to model your base material.

If you actually don't know which is the weak link, base or beam or fasteners, then the problem is much more complex because you can't model any of them as ideally rigid. I think most folks in this situation would use finite element modelling software and not formula based calculations.

The lifting force comes from the moment divided by the distance between the center of the beam and the fastening point, I think.

All I have right now is the force pushing the beam down and the tensile stress the bolts fail if fixed to concrete.

If nothing is pushing the vertical-with-repsect-gravity beam from side to side, then there is no moment and hence no lifting force. The concrete may crumble if the beam is too heavy, I guess. I don't know how to calculate that, though, you may be able to Google something useful about concrete properties.

edit: I see in your initial diagram you mean there is a cantilevered force at the top of the beam. You can get the lifting force by calculating the moment at the base of the beam and then dividing by the distance to the fastening point, as I said above.

Look here -

https://www.engineeringtoolbox.com/cantilever-beams-d_1848.html

to see how to calculate the moment if there is transverse force acting on the beam.

 

[Thomas Plank]

I see.

I don't know how you can find appropriate bulk material properties to model your base material.

If you actually don't know which is the weak link, base or beam or fasteners, then the problem is much more complex because you can't model any of them as ideally rigid. I think most folks in this situation would use finite element modelling software and not formula based calculations.

The lifting force comes from the moment divided by the distance between the center of the beam and the fastening point, I think.



If nothing is pushing the vertical-with-repsect-gravity beam from side to side, then there is no moment and hence no lifting force. The concrete may crumble if the beam is too heavy, I guess. I don't know how to calculate that, though, you may be able to Google something useful about concrete properties.

edit: I see in your initial diagram you mean there is a cantilevered force at the top of the beam. You can get the lifting force by calculating the moment at the base of the beam and then dividing by the distance to the fastening point, as I said above.

Look here -

https://www.engineeringtoolbox.com/cantilever-beams-d_1848.html

to see how to calculate the moment if there is transverse force acting on the beam.

I've currently solved it like this; however I feel like what I did assumes that the overall forces equals zero or I've overly simplified the problem.
https://ibb.co/hSbbfd
I've input my numbers into it but it comes out as a negative lifting force which means I've probably done it wrong.

Thank you.

 

[JBA]

In simple form, ignoring the vertical member, this just a standard lever problem . All you need in order determine the value of Fb to offset F is: Fb = Fx / Z and Fb is the force on your bolt.

 

[Grinkle]

@JBA I was about to post the same, then I started thinking about the plate extending to the left that will also be supporting the moment. I am trying to come up with a second equation to relate the support of the plate to the support of the fastening bolt.

If the length of the plate to the left is "n", then does 1/2nF = FbZ?

I'm thinking the plate support against the moment has a triangular shape, hence the 1/2n. Sorry if that is clear as mud - I can't make a drawing where I am right now.

 

[JBA]

Good catch. My mistake, You are correct. Assuming the base plate is rigid then the the base rotation point is the base edge opposite to the bolts, not the center of the pole. As a result, if we are not concerned with the base plate to pole connection, then the correct Z length in my equation would be the distance from that opposite edge to Fb. The result will be a lower Fb load than from my original equation.

Edit: On further thought, the distance of the vertical load on the arm from the back edge is also reduced from x to x- (the distance to the edge from the pole center) further reducing the Fb force.

 

[Thomas Plank]

Thanks for the response guys, so essentially it’s a simple moments question.

@Grinkle sorry I’m not too sure I understand the 1/2nF part, I thought the moment is only relevant if the distance is perpendicular to the force? Or have I misunderstand along the way?

*Sorry I forgot to mention, N is the tensile force the bolts can take in cracked concrete and Rb or Fb is the lifting force.

Thank you.

 

[Grinkle]

I thought the moment is only relevant if the distance is perpendicular to the force?

On the side opposite the bolt, if there is a stiff plate on a rigid surface, there will be a gradually increasing reaction force that is proportional to distance from the beam center. This will help support the cantilevered F. The stiff plate is in the direction perpendicular to the force, as is the gradually increasing reactive force of the rigid surface on the stiff plate. Sorry still no picture possible.

If there is no plate on that (left) side, then all of the F / moment induced by F is supported only by the bolt on the side of the beam opposite the F.

Edit - I think @JBA 's description is easier to follow - the center of rotation becomes the end of the rigid plate, not the center of the beam.

 

[jrmichler]

Assuming that the beam is (bolted / welded / fastened) to a bracket that is (bolted / cast into / fastened to rebar) to concrete, then you have the following five calculations:

1) The strength of the beam.
2) The strength of the beam connection to the bracket.
3) The strength of the bracket.
4) The strength of the connection of the bracket to the concrete.
5) The strength of the concrete.

Each of those calculations is a separate calculation that stands on its own. The strength of the finished assembly is the strength of whichever of those five is the weakest.