When is the Maximum Angle for Viewing a Tower from an Airplane?

[mathmari]

Hey! :giggle:

An aeroplane flies over a tower of height $h> 0$ at height $H> h$. At what distance $x$ is the angle $\alpha$ at which the tower is seen from the aeroplane, maximum?
(You can use elementary geometry and that $\arctan'(x)=\frac{1}{1+x^2}$.)

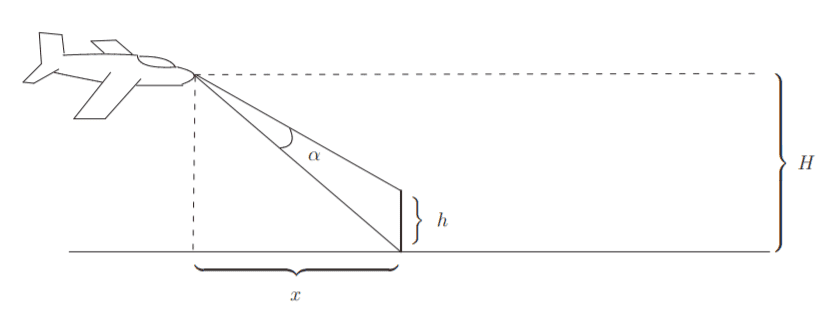From Pythagorean Theorem for the larger triangle we have that $H^2+x^2=:y^2$.

Do we apply for the smaller triangle law of cosine? But the upper side of that triangle is not known,and not related to the other triangle.

From the hint... Do we have to use somehow $\tan(\alpha)$ ?

:unsure:

 

[I like Serena]

Hey mathmari!

Suppose we use only tangents.
Which rectangular triangles can we find to apply the tangent to?

 

[mathmari]

Suppose we use only tangents.
Which rectangular triangles can we find to apply the tangent to?

We have the below rectangular triangle $ABC$ :

So we get $\tan (\phi)=\frac{x}{AB}$, right?

But we have to relate it with angle $\alpha$, right? Or do we have to consider an other triangle?

:unsure:

 

[I like Serena]

So we get $\tan (\phi)=\frac{x}{AB}$, right?

But we have to relate it with angle $\alpha$, right? Or do we have to consider an other triangle?

AB is the same as H isn't it? :unsure:

And yes, can we find another rectangular triangle?

 

[mathmari]

AB is the same as H isn't it? :unsure:

And yes, can we find another rectangular triangle?

Do we take a line that passes through $C$ and the intersection point with the upper horizinal line is say $D$ (then $|CD|=H$) and we get the triangle $ACD$ ?

:unsure:

 

[I like Serena]

Do we take a line that passes through $C$ and the intersection point with the upper horizinal line is say $D$ (then $|CD|=H$) and we get the triangle $ACD$ ?

That triangle $ACD$ is congruent with $ABC$ isn't it? :unsure:

Can we find another rectangular triangle?
Perhaps if we draw extra help lines?

 

[mathmari]

Can we find another rectangular triangle?
Perhaps if we draw extra help lines?

I suppose that we have to use the two line that have the angle $\alpha$ in between, or not? :unsure:

 

[I like Serena]

I suppose that we have to use the two line that have the angle $\alpha$ in between, or not?

How about these triangles:
\begin{tikzpicture}[scale=2]
\coordinate[label=left:A] (A) at (0,3);
\coordinate[label=left:B] (B) at (0,0);
\coordinate[label=below:C] (C) at (4,0);
\coordinate[label=T] (T) at (4,1);
\coordinate[label=above right:T'] (Ta) at (0,1);
\draw[thick] (A) -- (B) -- (C) -- cycle;
\draw[thick] (A) -- (T) -- node[ right ] {h} (C) (Ta) -- (T);
\path (A) -- node[ left ] {H} (B) -- node[below] {x} (C) -- (A) (B) -- node[ right ] {h} (Ta);
\end{tikzpicture}

 

[mathmari]

How about these triangles:
\begin{tikzpicture}[scale=2]
\coordinate[label=left:A] (A) at (0,3);
\coordinate[label=left:B] (B) at (0,0);
\coordinate[label=below:C] (C) at (4,0);
\coordinate[label=T] (T) at (4,1);
\coordinate[label=above right:T'] (Ta) at (0,1);
\draw[thick] (A) -- (B) -- (C) -- cycle;
\draw[thick] (A) -- (T) -- node[ right ] {h} (C) (Ta) -- (T);
\path (A) -- node[ left ] {H} (B) -- node[below] {x} (C) -- (A) (B) -- node[ right ] {h} (Ta);
\end{tikzpicture}

Considering the triangle $AT'T$ we get $\tan (\angle T'AT)=\frac{x}{H-h}$.
Considering the triangle $ABC$ we get $\tan (\angle BAC)=\frac{x}{H}$.

We have that $\alpha=\angle T'AT-\angle BAC$. So we get $$\tan (\alpha)=\tan \left (\angle T'AT-\angle BAC \right )=\frac{\tan (\angle T'AT)-\tan (\angle BAC)}{1+\tan (\angle T'AT)\tan (\angle BAC)}=\frac{\frac{x}{H-h}-\frac{x}{H}}{1+\frac{x}{H-h}\frac{x}{H}}=\frac{\frac{xH-xH+xh}{H(H-h)}}{\frac{H(H-h)+x^2}{H(H-h)}}=\frac{xh}{H(H-h)+x^2}$$

Then we have that $\alpha(x)=\arctan \left (\frac{xh}{H(H-h)+x^2}\right )$.

To get the maximum $\alpha$ we calculate the roots of the first derivative :
$$\alpha'(x)=0 \Rightarrow \arctan' \left (\frac{xh}{H(H-h)+x^2}\right )=0\Rightarrow \frac{1}{1+\left (\frac{xh}{H(H-h)+x^2}\right )^2}=0$$

From thatequation we get the desiredvaluefor $x$. Is that correct? :unsure:

 

[I like Serena]

Shouldn't we apply the chain rule?

Alternatively we might also observe that $\alpha(x)$ takes on its maximum value iff $\tan\alpha(x)$ does.
Then we don't need the derivative of $\arctan$ at all.

Btw, we can also write $\alpha = \arctan \angle T'AT - \arctan \angle BAC$.

 

[mathmari]

Shouldn't we apply the chain rule?

Ahh yes.. So we have $$\alpha'(x)=0 \Rightarrow \arctan' \left (\frac{xh}{H(H-h)+x^2}\right )=0\Rightarrow \frac{1}{1+\left (\frac{xh}{H(H-h)+x^2}\right )^2}\cdot \left (\frac{xh}{H(H-h)+x^2}\right )'=0 $$ right? :unsure:

Btw, we can also write $\alpha = \arctan \angle T'AT - \arctan \angle BAC$.

How do we get that? :unsure:

 

[I like Serena]

Ahh yes.. So we have $$\alpha'(x)=0 \Rightarrow \arctan' \left (\frac{xh}{H(H-h)+x^2}\right )=0\Rightarrow \frac{1}{1+\left (\frac{xh}{H(H-h)+x^2}\right )^2}\cdot \left (\frac{xh}{H(H-h)+x^2}\right )'=0 $$ right?

Yep. (Nod)

How do we get that?

Oops. I meant $\alpha = \angle T'AT - \angle BAC = \arctan \frac x{H-h} - \arctan\frac x H$.

 

[mathmari]

Yep. (Nod)Oops. I meant $\alpha = \angle T'AT - \angle BAC = \arctan \frac x{H-h} - \arctan\frac x H$.

Thank you!