shashaeee
- 30
- 0
I'm having a hard time trying to picture the problem:
A charge of +2q is placed at the origin and a second charge of -q is placed at x= 3.0cm. Where can a third charge +Q be placed so that it experiences a zero force?
Here is how I picture the problem:
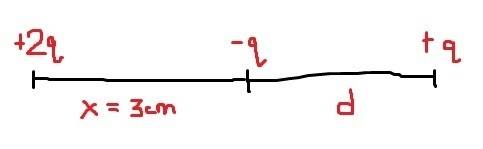
A charge of +2q is placed at the origin and a second charge of -q is placed at x= 3.0cm. Where can a third charge +Q be placed so that it experiences a zero force?
Here is how I picture the problem: