Where did I go wrong in finding the length x using the grabber-statics example?

AI Thread Summary
The discussion revolves around calculating the length x in a grabber-statics example, where the grabber must hold a box. The user initially derived two moment equations and combined them to find x but ended up with an incorrect result. They suspected a mistake related to the frictional force balancing the weight of the box and the normal force needed to create torque. After further analysis, they concluded that they had identified the error and arrived at the correct solution. The conversation highlights the importance of understanding the relationships between forces and torques in static equilibrium problems.
mrshlnnxfa
Messages
2
Reaction score
0
Hello,

We should get the length x , when the grabber can just hold the box.

yTBz.png


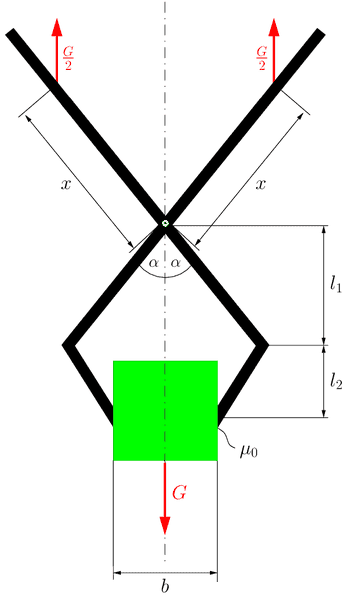
I made two moment equations:

e[czech]{babel}%20M_{1}=\frac{G}{2\mu%20}*\sqrt{(l_{1}+l_{2})^{2}+(\frac{b}{2})^{2}}\end{align*}.gif


yle\begin{align*}\usepackage[czech]{babel}%20M_{2}=\frac{G}{2}*\sin%20\alpha%20*%20x\end{align*}.gif


Then I put them together into one equation:
mathtex.gif


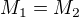
And from that equation I found out x:
mathtex.gif
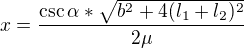Unfortunately the result seems to be wrong. Can you please help me? Where I made the mistake?
 
Engineering news on Phys.org
i think the frictional force balance the wight of the box.we have to give the normal force on the box that give rise to the friction by giving a torque to the grabber
 
I finally got it. Here is the solution.

Ehpw.png
 
Yes,that is the correct answer:smile:
 
Thread 'Physics of Stretch: What pressure does a band apply on a cylinder?'

Thread 'Physics of Stretch: What pressure does a band apply on a cylinder?'

Scenario 1 (figure 1) A continuous loop of elastic material is stretched around two metal bars. The top bar is attached to a load cell that reads force. The lower bar can be moved downwards to stretch the elastic material. The lower bar is moved downwards until the two bars are 1190mm apart, stretching the elastic material. The bars are 5mm thick, so the total internal loop length is 1200mm (1190mm + 5mm + 5mm). At this level of stretch, the load cell reads 45N tensile force. Key numbers...
View full post »

Thread 'Cantilever help'

I'm trying to decide what size and type of galvanized steel I need for 2 cantilever extensions. The cantilever is 5 ft. The space between the two cantilever arms is a 17 ft Gap the center 7 ft of the 17 ft Gap we'll need to Bear approximately 17,000 lb spread evenly from the front of the cantilever to the back of the cantilever over 5 ft. I will put support beams across these cantilever arms to support the load evenly
View full post »

Similar threads

Maximum load capacity of a time dependant Force on the surface of a metal
Replies
12
Views
2K
Election of cut placement for Shear flow -- Hibbeler's example
Replies
1
Views
1K
How to calculate how much energy a pneumatic system would need?
Replies
23
Views
2K
Body forces in static equilibrium (FEM issue)
Replies
2
Views
2K
Static Analysis Of Bolted Joints
Replies
12
Views
5K
Automotive How to find the uneven weight distribution on 4 wheels
Replies
5
Views
3K
Engineering Instantaneous Center of Rotation (Polplan in german) and STATICS
Replies
1
Views
1K
Volume of Static Solid Using Cross-Sectional Area (Integration)
Replies
2
Views
971
Plate - bending moment equation
Replies
2
Views
3K
I Statics: When the reactions depend on the displacements
Replies
35
Views
4K

Hot Threads

Recent Insights

Back
Top