Where Did I Go Wrong? Solving for Angular Momentum in Air Table Puck Collision

[ChiralSuperfields]

Homework Statement

Please see below

Relevant Equations

Please see below

For part(a),

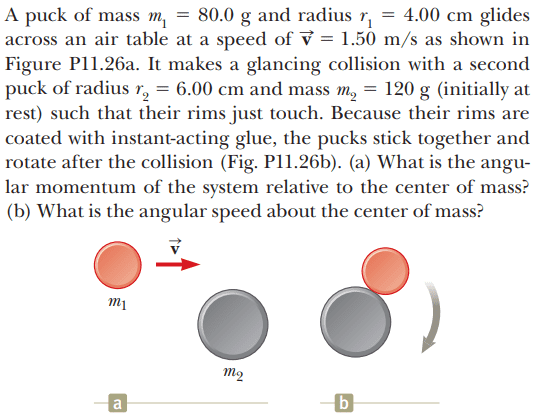
The solution is,

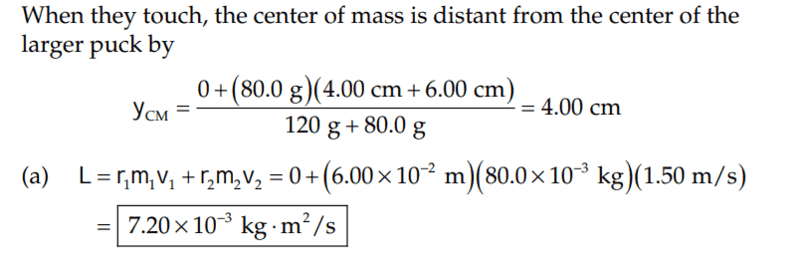
However, I made a mistake somewhere in my working below and I'm not sure what it is. Does anybody please know? Thank you!

Here is a not too scale diagram at the moment of the collision,

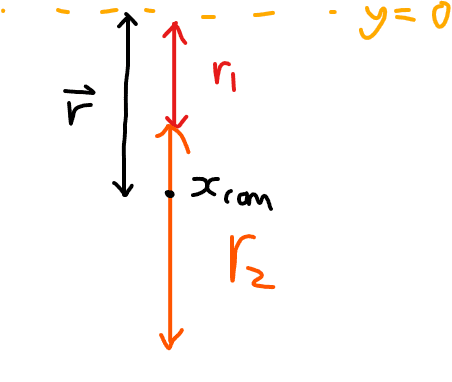
$\vec L = \vec r \times \vec p$
$\vec L = -y_{com}\hat j \times m_1v\hat i$
$\vec L = y_{com}m_1v\hat k$
$\vec L = \frac {m_2m_1v(r_1 +r_2)}{m_1 + m_2}\hat k$

 

[kuruman]

For part (a) please show what the distance $y_1$ from the CoM to the center of puck 1 is and how you got it in symbolic form.

 

[ChiralSuperfields]

For part (a) please show what the distance $y_1$ from the CoM to the center of puck 1 is and how you got it in symbolic form.

Thank you for your reply @kuruman!

I assume that the COM of each puck is at the geometric center.

Choosing the center of $m_1$ as the origin where $y = 0$ and let $r_3$ be the vertical distance from $y = 0$ to the COM of $m_2$.

$y_1 = y_{com} = \frac {m_1(0) + m_2r_3} {m_1 + m_2}$

$y_1 = \frac {m_2(r_1 + r_2)} {m_1 + m_2}$

Then substituting in values,

$y_1 = \frac {0.12(0.1)} {0.2}$
$y_1 = 0.06 m$

Also please see post #1, I missed some of the notations so I have edited it.

Many thanks!

 

[ChiralSuperfields]

Thank you for your help @kuruman! I see now how they got their answer. I think I got confused because the solutions calculated the $y_{com}$ from a different point. Good idea to use $y_1$ notation for calculations of CoM with respect to different origins!Many thanks!