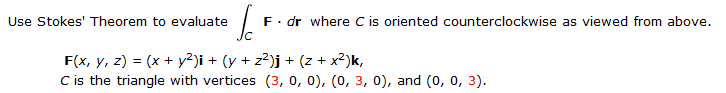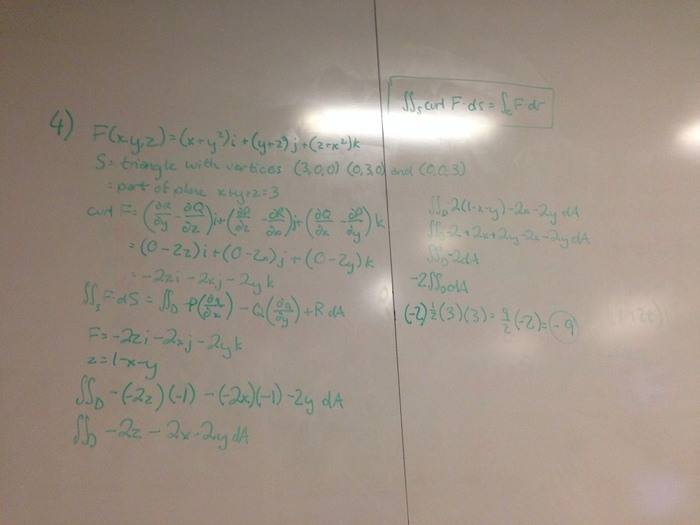Your picture is very difficult to read, but I solved it, and I think I can get you to the correct answer. This triangle has vertices at the 3 points, but what is the length of each side? (Hint: Each side does not have length 3). Also, this triangle lies in a plane. What is the unit vector ## \hat{n} ## normal to that plane? Be sure and properly normalize it. Now ## \nabla \times F \cdot \hat{n} ## is constant in the plane of the triangle, because the plane of the triangle has a simple equation (which you should be able to write out very quickly) and shows up in this ## \nabla \times F \cdot \hat{n} ## expression . (Please write out this equation for the plane of the triangle, so that it can be verified that you got it correct. It helps to see the calculations, and your picture is hard to read.) Finally, what is the height (altitude) of the equilateral triangle?, which you need to compute the area of the triangle, etc. Try again; I think you will be able to correct a mistake or two that you made.