Where Should the Bridges be Built to Minimize Road Length?

[Andreas C]

It's been a long time since I posted a riddle, and probably nobody missed them. Anyway, here is a collection of 3 well known geometry problems with different difficulty levels. The only reason there is an "I" prefix is because of the third part of the problem, which is a bit harder. The first one should be very easy, and the second one is probably high school level. For those confused with the story, read the previous riddles I posted (and the spoilers) to understand. I hope you enjoy it!

The Story
Following his arrest for his scam, Theseus You (Ok, it's kind of a dumb name) is led to the king. "You again??" he exclaims. "How did you manage to get into trouble again?". Theseus explains his story, and the king sits silently and thinks for a while. "Hmm..." the king says, "I can see that you're a clever and resourceful person, but dishonest. I should normally imprison you, but you might be of use. You will solve the following problem I have, otherwise you will be led to prison!".

The King's Problem
The king decided to build roads and bridges to connect the country. However, 3 villages separated by rivers and creeks are making it very hard for him, since their requirements are very specific and hard to meet.

Part I
Villages A and B are separated by a small creek in the shape of a straight line, and both villages want a watermill on the creek. Only 1 watermill can be built, and there will also be roads (which are straight lines) connecting the villages to the windmill. However, the villagers of A would be jealous if the road from the windmill to B was shorter than it was to them, and those of B would be jealous if it was shorter from the windmill to A than it was to them, so it was decided that the windmill should be built somewhere where the roads connecting the villages to it were both of the exact same length. Where should the windmill be built?

Part II
Villages B and C are separated by a river with a width of h. There will be 2 roads leading from each village to the river and a bridge to pass over it. The geography of the area is such that only a bridge that is perpendicular to both of the river banks (which are essentially 2 parallel lines) can be built. Where should the bridge be built so as to minimize the length of the road?

Part III
Villagers from village C often trade with a nearby castle with a circular moat of width q, and they want a road to be built to connect them to the castle. There has to be a bridge to pass over the moat, and that bridge has to point to the center of the circle (where the castle is). Where should the bridge be built to minimize the overall length of the road?

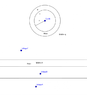
Here's a chart to help you understand:

IMPORTANT: If you want to post a solution, please do it with a spoiler, so that you don't ruin it for anyone who wants to solve one of these on his own!

 

[jedishrfu]

For the first problem:

Spoiler

draw a line thru A and B then make a perpendicular bisector to the line and where it intersects the stream...

For the second:

Spoiler

Draw a line thru B and C and where it intersects the river shorelines you use those two points to bisect the line and then draw a line perpendicular to the shorelines thru that point...

and for the third:

Spoiler

left to the future generations of geometers...

 

[Andreas C]

For the first problem:

Spoiler

draw a line thru A and B then make a perpendicular bisector to the line and where it intersects the stream...

For the second:

Spoiler

Draw a line thru B and C and where it intersects the river shorelines you use those two points to bisect the line and then draw a line perpendicular to the shorelines thru that point...

and for the third:

Spoiler

left to the future generations of geometers...

You got the first one right. The second one... You confused me a bit, what do you mean? Are you talking about bisecting the segment between the two intersecting points?

But yeah, the third one is hard. Let's see who solves it!

 

[mfb]

@jedishrfu: The second one does not work that way.
You can reduce it to the first one:

Spoiler

Note that the correct bridge position does not change if you shift B, the road from B to the bridge, and the southern river bank up by the same amount. Shift B up by the width of the river, then use the solution to problem A to find the ideal spot of the northern bridge head, build the bridge to find the southern bridge head position.

Part III [...] Where should the bridge be built to minimize the overall length of the road?

Clearly along the direct connection between the castle and C. The length of the bridge is constant, so minimizing the road length is equivalent to minimizing the total path length, and a direct connection is the shortest possible path (in Euclidean space).

 

[Andreas C]

Oh whoops, I just realized I posted the third problem wrong, the road isn't to the castle, it's to a post somewhere else (anywhere) inside the moat. I will correct it as soon as possible.