Which Vertex Angle Maximizes the Area of an Isosceles Triangle?

[calvinnn]

I posted this before, but i messed up on the wording, so here's my repost. My teacher gave us our problem of the week (which was previously on our test), and i have no idea on how to solve it. All i know is that i will probably need to differentiate something, and then find the criticle numbers. OK, so here it goes:

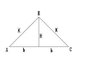
Use Calculus to prove which vertex angle gives an isosceles triangle the greatest area

Figure Below
THank You

 

[learningphysics]

Doesn't dextercioby give the solution here:
https://www.physicsforums.com/showthread.php?t=56279

 

[Tide]

I think you were already given the solution someplace else but perhaps you're looking for more detail?

The first question is do you have any contraints in the problem? For example, is the perimeter of the triangle fixed? I'd guess that the length of the equal sides is fixed since they are labled "K" which suggests a constant.

In that case the area of the triangle is

A = K^2 \sin \frac {\theta}{2} \cos \frac {\theta}{2} = \frac {1}{2}K^2 \sin \theta

where \theta is the vertex angle. Does that help?

 

[calvinnn]

thanks

things seem a bit clearer
Thanks