bergausstein
- 191
- 0
Hello! And Good day!
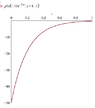
I just want to ask why do I keep getting a negative value whenever I take a definite integral of function $$y=-50e^{-5x}$$ the graph is shown as the first image.
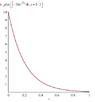
If you look at the graph of the integral of "y" there's no traceable negative value on the graph. Why is that? Please help me understand why. Thanks!
I just want to ask why do I keep getting a negative value whenever I take a definite integral of function $$y=-50e^{-5x}$$ the graph is shown as the first image.
If you look at the graph of the integral of "y" there's no traceable negative value on the graph. Why is that? Please help me understand why. Thanks!