Leo Liu
- 353
- 156
Sorry -- I think I have messed up the cross product. I just edited it.etotheipi said:Do let me know if I've misinterpreted something you said!
Unconstrained objects always rotate about their center of mass (CM) when tangential forces are applied due to the principles of classical mechanics. The net force acting on the object results in steady acceleration of the CM, adhering to Newton's first law. When external forces are applied, they create both translational and rotational effects, governed by the equations $$\sum \vec{F_{ext}}=m\vec{a_{CM}}$$ and $$\sum \vec{T_{ext}}=I\vec{\alpha}$$. The center of mass remains the inertial axis of rotation, ensuring that any deviation would contradict established physical laws.
PREREQUISITESPhysics students, mechanical engineers, and anyone interested in understanding the dynamics of rigid body motion and the principles governing rotation about the center of mass.
Sorry -- I think I have messed up the cross product. I just edited it.etotheipi said:Do let me know if I've misinterpreted something you said!
Leo Liu said:Summary:: Conceptual question on rotation.
Why do unconstrained objects always rotate about the lines passing through their CMs when tangential forces are applied to them? I understand that if an object does not rotate about its CM, then its rotation will decay to the rotation about the axis passing through its CM.
Vanadium 50 said:Uh, doesn't it roll in the direction of the applied force? Am I missing something?
Vanadium 50 said:I took F as horizontal, the way it was drawn.
Note that if you assume no slippage and don't care about the acceleration, just the direction, then it is just a geometric problem. You don't even need forces and moments of inertia.etotheipi said:@Leo Liu Sorry, your maths is indeed right, I hadn't realized you took torques about the point of contact. Welp!
I think I did not phrase my question in the way I intended. My question is that if you apply a constant force at a fixed point on an unconstrained roller, as the diagram (##\hat i \to \hat j## and diagram was not drawn to scale, sorry!) below for an example, what will happen.Delta2 said:A tangential force can make a rigid body rotate, if that's what you asking. And it will also accelerate the center of mass of the rigid body, unless there are other external forces that neutralize the first force .
Example: A disk with an axis fixed through its center of mass. If we apply a tangential force at the disk, the disk will start rotating around its center, but the disk will not do translational motion because the tangential force is neutralized from the force that the fixed axis applies to the disk (if we assume that the axis is also fixed to a not moving point) which is opposite and equal to the tangential force. However the rotational effect is not neutralized because the force from the fixed axis has zero torque (w.r.t to the center of the disk) while the tangential force has non-zero torque (w.r.t to the center of the disk).
Things become more interesting if the fixed axis doesn't pass through the CM of the disk but through an other point. Then the rotational effect will still be the same, with regards to the angular acceleration , however the force from the axis now will not be opposite and equal to the tangential force now . The vector sum of the latter two forces will be equal to the mass of the disk times the acceleration of the CM, as theorem 1 states, but now the acceleration of the CM will not be zero, because CM will rotate around the fixed axis which is located at another point of the disk.
Leo Liu said:Just one more question -- if a constant tangential force is applied, will it give us a circular trajectory?
You see the periodicity at the start, but angular velocity increases so the periods and amplitudes become smaller. After a while it looks like linear motion, but if you would zoom in, you would still see little wiggles.Delta2 said:Now I see what exactly you had in mind in post #22. The application point of tangential force follows the rotation of the disk, which means that the tangential force keeps changing direction. Still this means that the tangential force has some sort of periodicity and i would expect this to show up in the plots.
Yes, if you play around with the moment of inertia to mass ratio or the lever arm of the force, you should be able to get more pronounced wiggles.Delta2 said:You 've setup all the parameters equal to 1, which doesn't help to spot the periodic behavior of motion.
As a supplement to making static plots I recommend playing around with dynamic simulations, to gain intuition on how things behave, when forces are applied to them:Leo Liu said: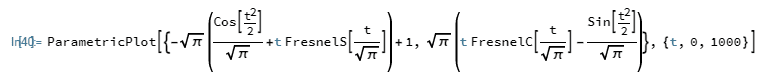
Thank you. I will try them for sure but I am not very confident with my programming skills lol.A.T. said:As a supplement to making static plots I recommend playing around with dynamic simulations, to gain intuition on how things behave, when forces are applied to them:
For the younger audience. It's never too early to train your physical intuition.Leo Liu said:Wait BAG PIGGIES? ARE YOU SERIOUS?
That will work too, I guess.Leo Liu said:I think I am going to just use wolfram's built-in animation.
A somewhat off-topic question: I have Mathematica and one can very easily make animations like the one you seem to have in mind.Leo Liu said:Okay never mind -- they are just games. Wait BAD PIGGIES? ARE YOU SERIOUS?
I think I am going to just use wolfram's built-in animation.
I have been using Wolfram's cloud computing and I had the same problem. To upload the animation I recorded my screen and converted it into gif format using a free online tool (not an ads).vanhees71 said:A somewhat off-topic question: I have Mathematica and one can very easily make animations like the one you seem to have in mind.
Does anybody know, how to export these animations to something one can distribute (like a gif movie or mp4 or whatever common format). The last time I tried, I could only manage to export it to a mov movie which was GB (sic) large, which is not feasible for a little animated plot ;-)).
A mass rotates around its CM because rotating around its CM is the only rotation point that doesn't require an additional counter-balancing force, which would be necessary to maintain rotation around any non-CM point.Leo Liu said:Summary:: Conceptual question on rotation.
Why do unconstrained objects always rotate about the lines passing through their CMs when tangential forces are applied to them? I understand that if an object does not rotate about its CM, then its rotation will decay to the rotation about the axis passing through its CM.
Also, when a roller rolling down from a banked surface, the static friction not only acts on the edge of the roller, which makes the roller rotate, but it exerts a translational acceleration opposing the gravity (##\vec{F_{net}} = \vec{F_{component \: of \: gravity}}+\vec{f_{static}}##). Why is it so?
Thanks.
Why would you need a counter-balancing force? The rotation just simply accelerates.Chris S said:A mass rotates around its CM because rotating around its CM is the only rotation point that doesn't require an additional counter-balancing force, which would be necessary to maintain rotation around any non-CM point.
Leo Liu said:Why would you need a counter-balancing force? The rotation just simply accelerates.
1) a free rigid body is not obliged to have a fixed axis of rotation;Leo Liu said:Summary:: Conceptual question on rotation.
Why do unconstrained objects always rotate about the lines passing through their CMs when tangential forces are applied to them? I understand that if an object does not rotate about its CM, th
Can you please explain what this means?wrobel said:a free rigid body is not obliged to have a fixed axis of rotation;
Why? Can you give me a proof?wrobel said:instantaneous axis of rotation is not obliged to pass through the center of mass.
@wrobel is using a axis of rotation to mean the set of points on a rigid body that are instantaneously at rest in a given inertial frame of reference.Leo Liu said:Can you please explain what this means?
Does object rotate about center of mass only if external forces dont exist and in case where sum of all external forces=0 ?jbriggs444 said:I want to expand a bit on @Dale's pithy response in #2 while staying away from the math in @Delta2's response in #4.
The idea is that we have this object. It has been subject to a tangential force but we remove the force and look at its motion. What axis is it now rotating around?
Well, what does it mean to say that the object is rotating around a particular axis? Likely what you have in mind is that there is a single point on the object that is moving at a constant speed in a straight line and that all of the other points on the object are rotating around that single point in lock step.
Since we removed the external force, the center of mass of the object is guaranteed to be moving in a straight line at a constant speed. So it would make a good axis. As @Dale points out, if some other point were the axis, moving in a straight line at a constant speed, then the center of mass would be moving around that point -- in violation of Newton's laws.
Isnt here air drag, external force?vanhees71 said:It's also rotating around the center of mass, if it's free falling in a constant gravitational field (as is usually a good approximation for motion close to the surface of the Earth).
Yes that make sense.vanhees71 said:I said "free falling". If there's air drag, it's not freely falling ;-))