Why do objects always rotate about their centre of mass?

[Leo Liu]

Do let me know if I've misinterpreted something you said!

Sorry -- I think I have messed up the cross product. I just edited it.

 

[PeroK]

Summary:: Conceptual question on rotation.

Why do unconstrained objects always rotate about the lines passing through their CMs when tangential forces are applied to them? I understand that if an object does not rotate about its CM, then its rotation will decay to the rotation about the axis passing through its CM.

Imagine any rigid body. Take the frame of reference in which the centre of mass is at rest. The only possible configurations for that object are rotations. There are no other possibilities.

Now take any point on that body and consider the frame of reference in which that point is at rest. Again, the only possible configurations for the object in that frame of reference are rotations.

If the body is rigid, there are no other configurations that preserve the original shape. One you remove any translational motion, rotations are the only possibilities that remain.

 

[etotheipi]

Uh, doesn't it roll in the direction of the applied force? Am I missing something?

Prof. Lewin has a good video on it, the direction of rotation depends on the angle of the string to the horizontal:

 

[Vanadium 50]

I took F as horizontal, the way it was drawn.

 

[etotheipi]

I took F as horizontal, the way it was drawn.

Yeah in that case it does indeed roll in the direction of the applied force. Around the 4:30 mark you can see the demo. It's just a slightly curious example of the rotation not being in the direction of the torque you apply .

@Leo Liu Sorry, your maths is indeed right, I hadn't realized you took torques about the point of contact. Welp!

 

[A.T.]

@Leo Liu Sorry, your maths is indeed right, I hadn't realized you took torques about the point of contact. Welp!

Note that if you assume no slippage and don't care about the acceleration, just the direction, then it is just a geometric problem. You don't even need forces and moments of inertia.

 

[Leo Liu]

A tangential force can make a rigid body rotate, if that's what you asking. And it will also accelerate the center of mass of the rigid body, unless there are other external forces that neutralize the first force .

Example: A disk with an axis fixed through its center of mass. If we apply a tangential force at the disk, the disk will start rotating around its center, but the disk will not do translational motion because the tangential force is neutralized from the force that the fixed axis applies to the disk (if we assume that the axis is also fixed to a not moving point) which is opposite and equal to the tangential force. However the rotational effect is not neutralized because the force from the fixed axis has zero torque (w.r.t to the center of the disk) while the tangential force has non-zero torque (w.r.t to the center of the disk).

Things become more interesting if the fixed axis doesn't pass through the CM of the disk but through an other point. Then the rotational effect will still be the same, with regards to the angular acceleration , however the force from the axis now will not be opposite and equal to the tangential force now . The vector sum of the latter two forces will be equal to the mass of the disk times the acceleration of the CM, as theorem 1 states, but now the acceleration of the CM will not be zero, because CM will rotate around the fixed axis which is located at another point of the disk.

I think I did not phrase my question in the way I intended. My question is that if you apply a constant force at a fixed point on an unconstrained roller, as the diagram ($\hat i \to \hat j$ and diagram was not drawn to scale, sorry!) below for an example, what will happen.

I think I already found an answer to my question. I used MMA to plot the path traveled by the roller. I set all parameter to 1 and set the time range from 0 to 5. This is what I got:

Setting time range from 0 to 10 gives me this:

Long-term behaviour:

(As you can see, the motion gradually becomes linear, which is interesting.)
However, I do not understand why it starts from (-1, 0) instead of (1, 0). So I am going to upload my work which I would like you to inspect, thanks. (I realized that the vector-valued function starts at (1, 0) instead of the origin when I was running.)

Follow-up:
My work is as follows:
Assuming that the roller starts from (0, 0), the initial force vector is $\hat j$ and r=moment arm.
$$\frac {\mathrm{d^2} \theta} {\mathrm d {t}^2}=\alpha$$
$$\therefore I\frac {\mathrm{d^2} \theta} {\mathrm d {t}^2}=rF \: (F \: is \: the \: magnitude \: of \: \vec F)$$
$$\theta(t)=\int \int \frac{rF}{I} \mathrm d t \mathrm d t$$
$$\theta(t)=\frac{rFt^2}{2I}$$
Now I am going to use a vector-valued function to express $\vec F$
$$\vec{F}(\theta)=-F \cdot \sin(\theta) \hat i + F \cdot \cos(\theta) \hat j$$
The Sin function is used to express Fx because $\cos(\theta + \frac \pi 2)=-\sin(\theta)$. Likewise, Cos function is used to express Fy because $\sin(\theta + \frac \pi 2)=\cos(\theta)$. (Adding pi over two because the initial force vector is perpendicular to the x axis)
$$\therefore \vec{a}(\theta) = -\frac F m \cdot \sin(\theta) \hat i + \frac F m \cdot \cos(\theta) \hat j$$
$$\therefore \vec{x}(t)= \int \int -\frac F m \cdot \sin(\frac{rFt^2}{2I}) \mathrm d t \: \mathrm d t \: \hat i + \int \int \frac F m \cdot \cos(\frac{rFt^2}{2I}) \mathrm d t \: \mathrm d t \: \hat j$$
Then I used MMA to solve these double integrals.
Set all parameters to 1:

Evaluate the i integral:

Evaluate the j integral:

Plot:

(the solution to the j integral is added by 1 because the initial position of the force is (1, 0) and the initial position of the CM is (0, 0))
And this gives me the graph.

 

[Delta2]

Now I see what exactly you had in mind in post #22. The application point of tangential force follows the rotation of the disk, which means that the tangential force keeps changing direction. Still this means that the tangential force has some sort of periodicity and i would expect this to show up in the plots. You 've setup all the parameters equal to 1, which doesn't help to spot the periodic behavior of motion.

 

[Stephen Tashi]

Just one more question -- if a constant tangential force is applied, will it give us a circular trajectory?

A constant force is also constant in direction. Are you asking what happens if a constant force is applied to the same point on an object? If so, what would that force be tangential to?

 

[A.T.]

Now I see what exactly you had in mind in post #22. The application point of tangential force follows the rotation of the disk, which means that the tangential force keeps changing direction. Still this means that the tangential force has some sort of periodicity and i would expect this to show up in the plots.

You see the periodicity at the start, but angular velocity increases so the periods and amplitudes become smaller. After a while it looks like linear motion, but if you would zoom in, you would still see little wiggles.

 

[A.T.]

You 've setup all the parameters equal to 1, which doesn't help to spot the periodic behavior of motion.

Yes, if you play around with the moment of inertia to mass ratio or the lever arm of the force, you should be able to get more pronounced wiggles.

 

[A.T.]

As a supplement to making static plots I recommend playing around with dynamic simulations, to gain intuition on how things behave, when forces are applied to them:

http://www.algodoo.com/

Or even this:

https://play.google.com/store/apps/details?id=com.rovio.BadPiggies

 

[Leo Liu]

As a supplement to making static plots I recommend playing around with dynamic simulations, to gain intuition on how things behave, when forces are applied to them:

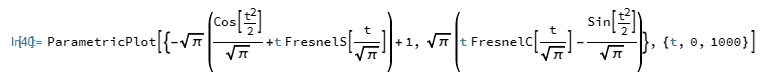
Thank you. I will try them for sure but I am not very confident with my programming skills lol.

Anyway, I created a plot to visualize the path traveled by the point at which the constant tangential force is applied. I think it is kind of fun.

Edit:
Okay never mind -- they are just games. Wait BAD PIGGIES? ARE YOU SERIOUS?
I think I am going to just use wolfram's built-in animation.

 

[A.T.]

Wait BAG PIGGIES? ARE YOU SERIOUS?

For the younger audience. It's never too early to train your physical intuition.

I think I am going to just use wolfram's built-in animation.

That will work too, I guess.

 

[vanhees71]

Okay never mind -- they are just games. Wait BAD PIGGIES? ARE YOU SERIOUS?
I think I am going to just use wolfram's built-in animation.

A somewhat off-topic question: I have Mathematica and one can very easily make animations like the one you seem to have in mind.

Does anybody know, how to export these animations to something one can distribute (like a gif movie or mp4 or whatever common format). The last time I tried, I could only manage to export it to a mov movie which was GB (sic) large, which is not feasible for a little animated plot ;-)).

 

[Leo Liu]

A somewhat off-topic question: I have Mathematica and one can very easily make animations like the one you seem to have in mind.

Does anybody know, how to export these animations to something one can distribute (like a gif movie or mp4 or whatever common format). The last time I tried, I could only manage to export it to a mov movie which was GB (sic) large, which is not feasible for a little animated plot ;-)).

I have been using Wolfram's cloud computing and I had the same problem. To upload the animation I recorded my screen and converted it into gif format using a free online tool (not an ads).

However, I do not know how to add a line between the two points to show the moment arm, which is a pity.

 

[vanhees71]

That's a great idea! Thanks!

 

[Chris S]

Summary:: Conceptual question on rotation.

Why do unconstrained objects always rotate about the lines passing through their CMs when tangential forces are applied to them? I understand that if an object does not rotate about its CM, then its rotation will decay to the rotation about the axis passing through its CM.

Also, when a roller rolling down from a banked surface, the static friction not only acts on the edge of the roller, which makes the roller rotate, but it exerts a translational acceleration opposing the gravity ($\vec{F_{net}} = \vec{F_{component \: of \: gravity}}+\vec{f_{static}}$). Why is it so?

Thanks.

A mass rotates around its CM because rotating around its CM is the only rotation point that doesn't require an additional counter-balancing force, which would be necessary to maintain rotation around any non-CM point.

 

[Leo Liu]

A mass rotates around its CM because rotating around its CM is the only rotation point that doesn't require an additional counter-balancing force, which would be necessary to maintain rotation around any non-CM point.

Why would you need a counter-balancing force? The rotation just simply accelerates.

 

[etotheipi]

Why would you need a counter-balancing force? The rotation just simply accelerates.

I think what he means is that, for instance, if you spin up the the rigid body, let go, and let it rotate about a fixed axis not through the centre of mass, you will need to allow for a contact force at the axis to provide the radial acceleration of the centre of mass.

But if the rigid body rotates under the action of no external forces about an axis through the centre of mass, there will be no contact force required.

 

[wrobel]

Summary:: Conceptual question on rotation.

Why do unconstrained objects always rotate about the lines passing through their CMs when tangential forces are applied to them? I understand that if an object does not rotate about its CM, th

1) a free rigid body is not obliged to have a fixed axis of rotation;
2) instantaneous axis of rotation is not obliged to pass through the center of mass.
All these things can change from one inertial frame to another one.

 

[Leo Liu]

a free rigid body is not obliged to have a fixed axis of rotation;

Can you please explain what this means?

instantaneous axis of rotation is not obliged to pass through the center of mass.

Why? Can you give me a proof?

 

[jbriggs444]

Can you please explain what this means?

@wrobel is using a axis of rotation to mean the set of points on a rigid body that are instantaneously at rest in a given inertial frame of reference.

Consider, for instance, an ideal car wheel as the car rolls down the highway and use the frame of reference of the road. The axle is not instantaneously at rest. So it does not qualify as the axis of rotation in this sense.

The points that are at rest are at the contact patch of tire on road. So the "axis of rotation" as he uses the term would be the line of points running across the width of the tire where it meets the road. Obviously, this is only the axis of rotation for an instant. A little bit later the axis of rotation will be a new line a little bit further down the road.

You can see that if we changed to a frame of reference anchored to the car that the axis of rotation would then be at the axle.

 

[etotheipi]

Also, if we allow non-inertial frames, you could imagine a coordinate system with its origin fixed to a specific moving point on the tire, with axes always aligned with a coordinate system fixed in the road frame. The motion of the wheel in this frame is now restricted to rotations about this point, even though it is not the centre-of-mass!

 

[John Mcrain]

I want to expand a bit on @Dale's pithy response in #2 while staying away from the math in @Delta2's response in #4.

The idea is that we have this object. It has been subject to a tangential force but we remove the force and look at its motion. What axis is it now rotating around?

Well, what does it mean to say that the object is rotating around a particular axis? Likely what you have in mind is that there is a single point on the object that is moving at a constant speed in a straight line and that all of the other points on the object are rotating around that single point in lock step.

Since we removed the external force, the center of mass of the object is guaranteed to be moving in a straight line at a constant speed. So it would make a good axis. As @Dale points out, if some other point were the axis, moving in a straight line at a constant speed, then the center of mass would be moving around that point -- in violation of Newton's laws.

Does object rotate about center of mass only if external forces dont exist and in case where sum of all external forces=0 ?

 

[vanhees71]

It's also rotating around the center of mass, if it's free falling in a constant gravitational field (as is usually a good approximation for motion close to the surface of the Earth).

 

[John Mcrain]

It's also rotating around the center of mass, if it's free falling in a constant gravitational field (as is usually a good approximation for motion close to the surface of the Earth).

Isnt here air drag, external force?

 

[vanhees71]

I said "free falling". If there's air drag, it's not freely falling ;-)).

 

[John Mcrain]

I said "free falling". If there's air drag, it's not freely falling ;-))

Yes that make sense.

If gust of wind hit the arrow in flight from side, arrow will rotate with nose upwind,because of feathers at the back.

Is arrow rotate around c.m. during time to align with new apparent wind(head wind+side gust wind) and translate downwind?

 

[Dale]

Any infinitesimal rigid body motion can be described as an infinitesimal translation of any arbitrary material point on the body and an infinitesimal rotation about that point.

The thing that makes the center of mass special is not the rotation, that happens about every point. The thing that makes the center of mass special is that its translational motion is simple. Rotation occurs about every point, as does translation of that point. But the simple translation of the center of mass makes analysis easier if we choose that as our reference.