I'm not sure I understand your question, but let me illustrate how the integrals come into play by an analogy.
Suppose we are betting on a frog. We have a race track with a starting line at square number 0 and a finish line at square number 100. We put the frog at the starting line, and let the frog take 10 jumps. The frog wins if after 10 jumps, it has made it to the finish line. The oddsmakers need to figure out the probability of the frog winning. They can mathematically describe it by a function P(x, y, N), which is the probability that the frog can get from square x to square y in N jumps. Of course, the number that they are interested in is P(0,100,10). To compute P(x,y,N), they reason as follows:
- On the first jump, the frog will reach some square--0, 1, 2, ..., or 100.
- So there are 101 ways for the frog to win the race: Either he gets to 0 in 1 jump and gets from 0 to 100 in 9 more jumps, or he gets to 1 in 1 jump and gets to 100 in 9 more jumps, etc.
- The probability that the frog wins in the first way is: P(0, 0, 1) P(0, 100, 9)
- The probability that the frog wins in the second way is: P(0, 1, 1) P(1, 100, 9)
- etc.
- To compute the probability of the frog winning, we just add up the probabilities for each possible way of winning.
- So: P(0, 100, 10) = \sum_{x_1 = 0\ to\ 100} P(0, x_1, 1) P(x_1, 100, 9)
- Similarly, P(x_1, 100, 9) = \sum_{x_2 = 0\ to\ 100} P(x_1, x_2, 1) P(x_2, 100, 8)
- Continuing to break the number of jumps down, we come to the conclusion that: P(0, 100, 10) = \sum_{x_1} \sum_{x_2} \sum_{x_3} ... \sum_{x_{9} } P(0, x_1, 1) P(x_1, x_2, 1) ... P(x_9, 100, 1), where all the sums are from 0 to 100.
Now, the above calculation is actually an approximation, because we ignored the frog's position within a square. In reality, there is practically a continuum of positions that the frog can be at after one jump. So the summations should actually be replaced by integrals:
P(0, 100, 10) = \int_{x_1} \int_{x_2} \int_{x_3} ... \int_{x_{9} } dx_1 dx_2 ... dx_9 P(0, x_1, 1) P(x_1, x_2, 1) ... P(x_9, 100, 1), where all the integrals are from 0 to 100.
If we had a quantum-mechanical frog, then instead of computing probabilities, we would compute probability amplitudes: Let G(x,y,t) be the probability amplitude that the frog will move from x to y in t seconds. Then:
G(x, y, t) = \int_{x_1} \int_{x_2} \int_{x_3} ... \int_{x_{N-1} } dx_1 dx_2 ... dx_{N-1} G(x, x_1, \delta t) G(x_1, x_2, \delta t) ... G(x_9, y, \delta t)
where \delta t = t/N
To get the path integral, you write, in the case where \delta t is very small:
G(x,y,\delta) \approx C e^{\frac{i L(x,\dot{x}) \delta t}{\hbar}} where C is some normalization factor, and L(x, \dot{x}) is the classical Lagrangian, and \dot{x} = \frac{y - x}{\delta t}. Using properties of exponentials, we can rewrite this as
G(x, y, t) = \int_{x_1} \int_{x_2} \int_{x_3} ... \int_{x_{N-1} } dx_1 dx_2 ... dx_{N-1} C^{N-1} e^{\frac{i}{\hbar} \sum_{i=0\ to\ N} L(x, \dot{x}) \delta t}
The sum in the integral becomes an integral in the limit as \delta t \Rightarrow 0:
G(x, y, t) = \int_{x_1} \int_{x_2} \int_{x_3} ... \int_{x_{N-1} } dx_1 dx_2 ... dx_{N-1} C^{N-1} e^{\frac{i}{\hbar} \int_{0}^t L(x, \dot{x}) dt'}
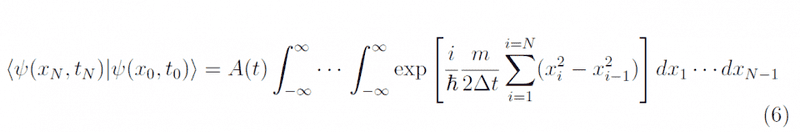
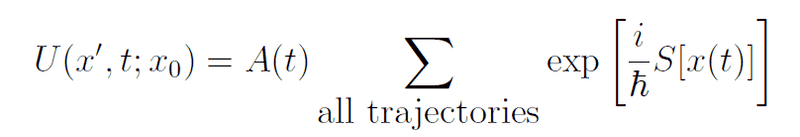but why do they instead multiply and integrate over integration and so on?Also for equation (7)
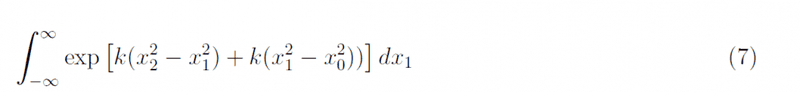, shouldn't it be this
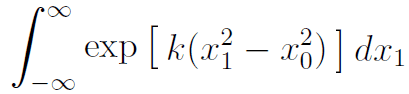instead?
